
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.
(1)求渔船甲的速度;
(2)求sinα的值.
(1)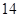 海里/小时;(2)
海里/小时;(2)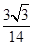 .
.
解析试题分析:(1)首先利用余弦定理求出BC,即可求出渔船甲的速度;
(2)由余弦定理求出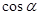 ,再利用同角及泵西求出
,再利用同角及泵西求出 .
.
试题解析:解:(1)依题意, ,
, ,
,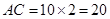 ,
, .
.
在△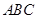 中,由余弦定理,得
中,由余弦定理,得
 .解得
.解得 . 4分
. 4分
所以渔船甲的速度为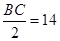 海里/小时.
海里/小时.
答:渔船甲的速度为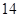 海里/小时. 6分
海里/小时. 6分
(2)在△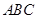 中,因为
中,因为 ,
, ,
, ,
, ,
,
由余弦定理,得 .即
.即 . 9分
. 9分
因为 为锐角,所以
为锐角,所以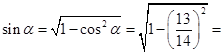
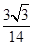 .
.
答: 的值为
的值为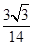 . 12分
. 12分
法二:在△ABC中,因为AB=12(海里),∠BAC=120°,BC=28(海里),∠BCA=α,由正弦定理,得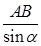 =
= .
.
即sinα=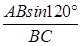 =
= =
=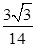 . 11分
. 11分
答: 的值为
的值为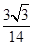 . 12分
. 12分
考点:1.正弦定理和余弦定理;2.同角的基本关系.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=(2cos2x-1)sin2x+ cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。
(2)设A,B,C为△ABC的三个内角,若cosB=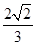 ,f(
,f(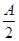 )=-
)=- ,且角A为钝角,求sinC
,且角A为钝角,求sinC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com