
分析 利用平面向量的数量积运算法则化简已知的不等式,得到两向量的夹角为锐角,从而得到三角形的内角为钝角,即可得到三角形为钝角三角形;反过来,三角形ABC若为钝角三角形,可得B不一定为钝角,故原不等式不一定成立,可得前者是后者的充分不必要条件.
解答 解:∵$\overrightarrow{AB}$•$\overrightarrow{BC}$>0,即|$\overrightarrow{AB}$|•|$\overrightarrow{BC}$|cosθ>0,
∴cosθ>0,且θ∈(0,π),
所以两个向量的夹角θ为锐角,
又两个向量的夹角θ为三角形的内角B的补角,
所以B为钝角,所以△ABC为钝角三角形,
反过来,△ABC为钝角三角形,不一定B为钝角,
则“$\overrightarrow{AB}$•$\overrightarrow{BC}$>0”是“△ABC为钝角三角形”的充分条件不必要条件.
故答案为:充分不必要.
点评 此题考查了三角形形状的判断,涉及的知识有平面向量的数量积运算,以及充分必要条件的证明,熟练掌握平面向量的数量积运算法则是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
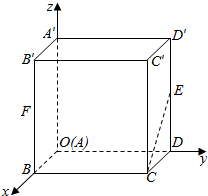 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多可运行台数 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com