
【题目】在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
参加跳绳的同学 | 未参加跳绳的同学 | |
参加踢毽的同学 | 9 | 4 |
未参加踢毽的同学 | 7 | 20 |
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)首先求得至少参加上述一项活动的同学有![]() 人,然后由古典概型公式求解概率为
人,然后由古典概型公式求解概率为![]() .
.
(2)利用题意写出所有可能的时间,由题意确定男同学甲未被选中且女同学乙被选中的事件的个数,然后利用公式求解概率为![]() .
.
试题解析:
解:(1)由表可知,既参加跳绳又参加踢毽的同学![]() 人,只参加踢毽的同学
人,只参加踢毽的同学![]() 人,
人,
只参加跳绳的同学![]() 人,所以至少参加上述一项活动的同学有
人,所以至少参加上述一项活动的同学有![]() 人.
人.
设“该同学至少参加上述一项活动”为事件![]() ,则
,则![]() .
.
(2)设5名男同学为甲,1,2,3,4;4名女同学为乙,5,6,7.
所有可能的结果有:(甲,乙),(甲,5),(甲,6),(甲,7),(1,乙),(1,5),(1,6),(1,7),(2,乙),(2,5),(2,6),(2,7),(3,乙),(3,5),(3,6),(3,7),(4,乙),(4,5),(4,6),(4,7),共计20种.
记“男同学甲未被选中且女同学乙被选中”为事件B,
则![]() 共包含(1,乙),(2,乙),(3,乙),(4,乙),共4个结果.
共包含(1,乙),(2,乙),(3,乙),(4,乙),共4个结果.
![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】下列命题中__________为真命题(把所有真命题的序号都填上).
①“![]() ”成立的必要条件是“
”成立的必要条件是“![]() ”;
”;
②“若![]() 成等差数列,则
成等差数列,则![]() ”的否命题;
”的否命题;
③“已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() 成等比数列.”的逆否命题;
成等比数列.”的逆否命题;
④“已知![]() 是
是![]() 上的单调函数,若
上的单调函数,若![]() ,则
,则![]() ”的逆命题.
”的逆命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式的大小关系正确的是( )
A.sin11°>sin168°
B.sin194°<cos160°
C.tan(﹣ ![]() )<tan(﹣
)<tan(﹣ ![]() )
)
D.cos(﹣ ![]() )>cos
)>cos ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题; 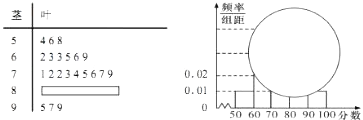
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
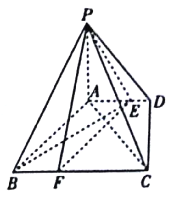
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com