[题目]某军工企业生产一种精密电子仪器的固定成本为20000元.每生产一台仪器需增加投入100元.已知总收益满足函数:其中x是仪器的月产量.(1)将利润表示为月产量的函数,(2)当月产量为何值时.公司所获利润最大?最大利润是多少元? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某军工企业生产一种精密电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：其中x是仪器的月产量.

（1）将利润表示为月产量的函数；

（2）当月产量为何值时，公司所获利润最大？最大利润是多少元？（总收益=总成本+利润.）

【答案】（1）；（2）当产量为300台时，公司获利润最大，最大利润为25000元．

【解析】

试题（1）根据题意总收益总成本利润，故利润总收益总成本，易得函数关系式；

（2）通过（1）知函数关系式为分段函数，故函数的最大值为各段最大值中的最大值．

试题解析：（1）因每月产量台故总成本为，

从而

（2）①当时，，

当时，．

②当时，为减函数，

∴，

故当月产量为300台时，利润最大，最大利润为元．

练习册系列答案

小学语文词语手册吉林教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在三棱锥P﹣ABC中．侧梭长均为4．底边AC=4．AB=2，BC=2 ，D．E分别为PC．BC的中点．〔I）求证：平面PAC⊥平面ABC．
（Ⅱ）求三棱锥P﹣ABC的体积；
（Ⅲ）求二面角C﹣AD﹣E的余弦值．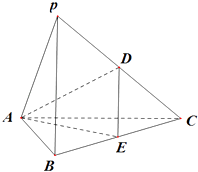

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某镇在政府“精准扶贫”的政策指引下，充分利用自身资源，大力发展养殖业，以增加收入，政府计划共投入72万元，全部用于甲、乙两个合作社，每个合作社至少要投入15万元，其中甲合作社养鱼，乙合作社养鸡，在对市场进行调研分析发现养鱼的收益、养鸡的收益与投入（单位：万元）满足 .设甲合作社的投入为（单位：万元）.两个合作社的总收益为（单位：万元）.

（1）当甲合作社的投入为25万元时，求两个合作社的总收益；

（2）试问如何安排甲、乙两个合作的投入，才能使总收益最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知是两条不同的直线，是两个不同的平面，则下列命题正确的是（）

A. 若，则 B. 若，则

C. 若，则 D. 若，则

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某地空气中出现污染，须喷洒一定量的去污剂进行处理.据测算，每喷洒1个单位的去污剂，空气中释放的浓度y（单位：毫克/立方米）随着时间x（单位：天）变化的函数关系式近似为，若多次喷洒，则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知，当空气中去污剂的浓度不低于4（毫克/立方米）时，它才能起到去污作用.

（Ⅰ）若一次喷洒4个单位的去污剂，则去污时间可达几天？

（Ⅱ）若第一次喷洒2个单位的去污剂，6天后再喷洒个单位的去污剂，要使接下来的4天中能够持续有效去污，试求的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂为了检查一条流水线的生产情况，从该流水线上随机抽取40件产品，测量这些产品的重量（单位：克），整理后得到如下的频率分布直方图（其中重量的分组区间分别为（490，495]，（495，500]，（500，505]，（505，510]，（510，515]）（I）若从这40件产品中任取两件，设X为重量超过505克的产品数量，求随机变量X的分布列；
（Ⅱ）若将该样本分布近似看作总体分布，现从该流水线上任取5件产品，求恰有两件产品的重量超过505克的概率．