
【题目】某校学生参加了“铅球”和“立定跳远”两个科目的体能测试,每个科目的成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为
五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为![]() 的学生有8人.
的学生有8人.

(Ⅰ)求该班学生中“立定跳远”科目中成绩为![]() 的人数;
的人数;
(Ⅱ)若该班共有10人的两科成绩得分之和大于7分,其中有2人10分,3人9分,5人8分.从这10人中随机抽取两人,求两人成绩之和![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)3人;(2)见解析.
【解析】试题分析:(Ⅰ)由“铅球”科目中成绩为E的学生有10人,频率为0.2,能求出该班有50人,由此能求出该班学生中“立定跳远”科目中成绩等级为A的人数.
(Ⅱ)设两人成绩之和为X,则X的值可能为:16,17,18,19,20,分别求出相应的概率,由此能求出X的分布列及EX.
解:(Ⅰ)∵“铅球”科目中成绩为E的学生有10人,频率为0.2,
∴该班有:![]() =50人,
=50人,
∴该班学生中“立定跳远”科目中成绩等级为A的人数为:
50(1﹣0.375﹣0.375﹣0.150﹣0.020)=4,
∴该班学生中“立定跳远”科目中成绩为A的人数为4人.
(Ⅱ)设两人成绩之和为X,则X的值可能为:16,17,18,19,20,
P(X=16)=![]() =
=![]() ,
,
P(X=17)=![]() =
=![]() ,
,
P(X=18)=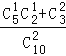 =
=![]() ,
,
P(X=19)=![]() =
=![]() ,
,
P(X=20)=![]() =
=![]() ,
,
∴X的分布列为:

EX=![]() =
=![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的x∈R,都有f(﹣x)+f(x)=﹣6,且当x≥0时,f(x)=2x﹣4,定义在R上的函数g(x)=a(x﹣a)(x+a+1),两函数同时满足:x∈R,都有f(x)<0或g(x)<0;x∈(﹣∞,﹣1),f(x)g(x)<0,则实数a的取值范围为( )
A.(﹣3,0)
B.![]()
C.(﹣3,﹣1)
D.(﹣3,﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点
=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点 ![]() .
.
(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某海面上有![]() 、
、![]() 、
、![]() 三个小岛(面积大小忽略不计),
三个小岛(面积大小忽略不计),![]() 岛在
岛在![]() 岛的北偏东
岛的北偏东![]() 方向
方向![]() 处,
处,![]() 岛在
岛在![]() 岛的正东方向
岛的正东方向![]() 处.
处.

(1)以![]() 为坐标原点,
为坐标原点,![]() 的正东方向为
的正东方向为![]() 轴正方向,
轴正方向,![]() 为单位长度,建立平面直角坐标系,写出
为单位长度,建立平面直角坐标系,写出![]() 、
、![]() 的坐标,并求
的坐标,并求![]() 、
、![]() 两岛之间的距离;
两岛之间的距离;
(2)已知在经过![]() 、
、![]() 、
、![]() 三个点的圆形区域内有未知暗礁,现有一船在
三个点的圆形区域内有未知暗礁,现有一船在![]() 岛的南偏西
岛的南偏西![]() 方向距
方向距![]() 岛
岛![]() 处,正沿着北偏东
处,正沿着北偏东![]() 行驶,若不改变方向,试问该船有没有触礁的危险?
行驶,若不改变方向,试问该船有没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°;
其中正确的是(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分) 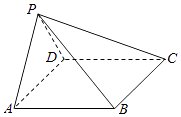
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() .
.
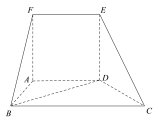
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 交于点
交于点![]() .
.
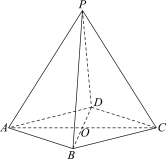
(Ⅰ)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() (异于点
(异于点![]() ),使得
),使得![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com