
����Ŀ�����Ա����ϣ�ij����ר��Т��ij���ز����������ľ���������������������أ����ز�ÿ�յ�������y����λ��ǧ�ˣ������ۼ۸�x����λ��Ԫ/ǧ�ˣ�1��x��5�����㣺��1��x��3ʱ��y=a��x��3��2+ ![]() ����a��bΪ����������3��x��5ʱ��y=��70x+490����֪�����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ÿ�տ��۳����ز�600ǧ�ˣ������ۼ۸�Ϊ3Ԫ/ǧ��ʱ��ÿ�տ��۳�150ǧ�ˣ�
����a��bΪ����������3��x��5ʱ��y=��70x+490����֪�����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ÿ�տ��۳����ز�600ǧ�ˣ������ۼ۸�Ϊ3Ԫ/ǧ��ʱ��ÿ�տ��۳�150ǧ�ˣ�
��1����a��b��ֵ����ȷ��y����x�ĺ�������ʽ��
��2�������ز������۳ɱ�Ϊ1Ԫ/ǧ�ˣ���ȷ�����ۼ۸�x��ֵ��ʹ����ÿ�����۸��ز���������f��x�����x��ȷ��0.1Ԫ/ǧ�ˣ���
���𰸡�
��1���⣺�����⣺
x=2ʱy=600����a+b=600��
�֡�x=3ʱy=150����b=300��
�� 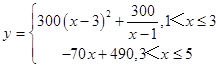
��2���⣺�����⣺
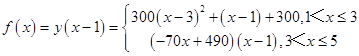 ��
��
��1��x��3ʱ��
f��x��=300��x��3��2��x��1��+300=300��x3��7x2+15x��8����
f'��x��=300��3x2��14x+15��=��3x��5����x��3����
�� ![]() ʱ�����ֵ
ʱ�����ֵ ![]() ��
��
��3��x��5ʱ��
f��x��=����70x+490����x��1����
��x=4ʱ�����ֵ630��
��630�� ![]() ��
��
�൱ ![]() ʱf��x�������ֵ
ʱf��x�������ֵ ![]() ��
��
�������ۼ۸�Ϊ1.7Ԫ��ֵ��ʹ���������������
����������1�������⣬�����������a��b���Ӷ���������Ľ���ʽ����2�������Ƿֶκ���������������ֵ����ֵ���Ӷ����������ֵ�㣮


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������BCDP�У�BC��PD��BA��PD�ڵ�A��PD=3BC����AB=BC=1����AB�ѡ�PAB����P'AB��λ�ã���ͼ2����ʹ��P'AD=90�㣮 ������֤��CD��ƽ��P'AC��
����������A��P'D��C������ֵ��
�����߶�P'A���Ƿ���ڵ�M��ʹ��BM��ƽ��P'CD�������ڣ�ָ����M��λ�ò�֤�����������ڣ���˵�����ɣ�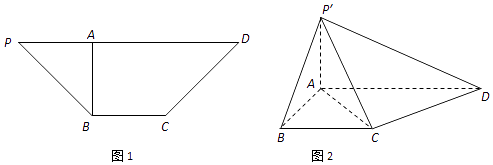
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2sin����x+�գ����أ�0��0���գ��У���ͼ��������������ߵ�ľ���Ϊ�У���������f��x����ͼ������ƽ�� ![]() ����λ���Ⱥ�����ͼ�����y��Գƣ�����f��x���Ľ���ʽΪ�� ��
����λ���Ⱥ�����ͼ�����y��Գƣ�����f��x���Ľ���ʽΪ�� ��
A.f��x��=2sin��x+ ![]() ��
��
B.f��x��=2sin��x+ ![]() ��?
��?
C.f��x��=2sin��2x+ ![]() ��
��
D.f��x��=2sin��2x+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x�������ڶ������ڴ���x0 �� ʹ��f����x0��=��f��x0�����������x0Ϊ����f��x���ľֲ��ԳƵ㣮
��I����a��R��a��0������f��x��=ax2+x��a�ġ��ֲ��ԳƵ㡱��
��II��������f��x��=4x��m2x+1+m2��3��R���оֲ��ԳƵ㣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cos��x+ ![]() ������Ҫ�õ��䵼����y=f�䣨x����ͼ��ֻ�轫����y=f��x����ͼ�� ��
������Ҫ�õ��䵼����y=f�䣨x����ͼ��ֻ�轫����y=f��x����ͼ�� ��
A.����ƽ�� ![]() ����λ
����λ
B.����ƽ�� ![]() ����λ
����λ
C.����ƽ�� ![]() ����λ
����λ
D.����ƽ�� ![]() ����λ
����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ķ������ǣ�0��+�ޣ���f'��x��Ϊf��x���ĵ�������������f��x����f'��x������ʽ ![]() f��2���Ľ⼯�ǣ� ��
f��2���Ľ⼯�ǣ� ��
A.�����ޣ�2���ȣ�1��+�ޣ�
B.����2��1��
C.�����ޣ���1���ȣ�2��+�ޣ�
D.����1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=alnx��x+1��a��R����
��������f��x���ĵ������䣻
������������x�ʣ�0��+�ޣ�������f��x����0����ʵ��a��ȡֵ��Χ��
����֤�� ![]() ������n��N* �� eΪ��Ȼ�����ĵ�������
������n��N* �� eΪ��Ȼ�����ĵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC1�� ![]() =1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ����F2Ҳ��������C2��y2=4x�Ľ��㣬M��C1��C2�ڵ�һ���Ľ��㣬��
=1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ����F2Ҳ��������C2��y2=4x�Ľ��㣬M��C1��C2�ڵ�һ���Ľ��㣬�� ![]()
��I������ԲC1�ķ��̣�
������֪����ABCD�Ķ���A��C����ԲC1�ϣ�����B��D��ֱ��7x��7y+1=0�ϣ���ֱ��AC�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����PΪ����C1�϶��㣬QΪ����C2�϶��㣬���|PQ|����СֵΪ����C1 �� C2֮��ľ��룬����d��C1 �� C2������C1��x2+y2=2��C2����x��3��2+��y��3��2=2����d��C1 �� C2��=����C3��ex��2y=0��C4��lnx+ln2=y����d��C3 �� C4��= ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com