
【题目】已知函数f(x)![]() (k>0)
(k>0)
(1)若f(x)>m的解集为{x|x<-3,或x>-2},求不等式5mx2+kx+3>0的解集;
(2)若存在x>3,使得f(x)>1成立,求k的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据不等式解集与对应方程根的关系:-3,-2是方程mx2-2kx+6km=0的根,即利用韦达定理得方程组,解方程组可得m,k的值,代入不等式5mx2+kx+3>0再解一元二次不等式即可(2)不等式有解问题,一般转化为对应函数最值问题: 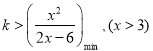 ,再根据基本不等式求最值,即得k的取值范围.
,再根据基本不等式求最值,即得k的取值范围.
试题解析:解:(1)不等式![]() ,
,
∵不等式mx2-2kx+6km<0的解集为{x|x<-3,或x>-2},∴-3,-2是方程mx2-2kx+6km=0的根,
∴![]() ,故有
,故有![]() ,
,
∴不等式5mx2+kx+3>0的解集为![]() .
.
(2)![]() .
.
存在x>3,使得f(x)>1成立,即存在x>3,使得![]() 成立.
成立.
令![]() ,则k>g(x)min.
,则k>g(x)min.
令2x-6=t,则t∈(0,+∞),![]() ,
,
当且仅当![]() 即
即![]() 时等号成立.
时等号成立.
∴![]() ,故k∈(6,+∞).
,故k∈(6,+∞).


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lg(ax2+2x+1) .
(1)若函数f (x)的定义域为R,求实数a的取值范围;
(2)若函数f (x)的值域为R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高2010级数学培优学习小组有男生3人女生2人,这5人站成一排留影。
(1)求其中的甲乙两人必须相邻的站法有多少种?
(2)求其中的甲乙两人不相邻的站法有多少种?
(3)求甲不站最左端且乙不站最右端的站法有多少种 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 为参数)与曲线
为参数)与曲线![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 中点
中点![]() 的坐标;
的坐标;
(2)若![]() ,其中
,其中![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为![]() ,用某种数学方法到处等价的形式
,用某种数学方法到处等价的形式![]() ,然后按以下步骤执行:
,然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量![]() ;
;
(2)将![]() 的值保存于变量
的值保存于变量![]() ,然后计算
,然后计算![]() ,并将结果存于变量
,并将结果存于变量![]() ;
;
(3)当![]() 与
与![]() 的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的
的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的![]() 就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系![]() 中, 直线
中, 直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .
.
(1)写出曲线![]() 直角坐标方程和直线
直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
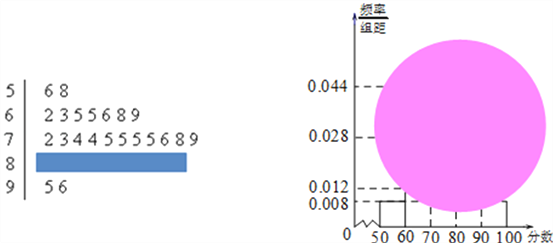
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,![]() 轴为正半轴建立极坐标系,圆
轴为正半轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为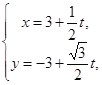 (t为参数).
(t为参数).
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)求直线![]() 分圆
分圆![]() 所得的两弧程度之比.
所得的两弧程度之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com