
ЎҫМвДҝЎҝДі№Өі§ЙъІъјЧЎўТТБҪЦЦІъЖ·ЛщөГөДАыИу·ЦұрОӘ![]() әН
әН![]() ЈЁНтФӘЈ©Ј¬КВПИёщҫЭПа№ШЧКБПөГіцЛьГЗУлН¶ИлЧКҪр
ЈЁНтФӘЈ©Ј¬КВПИёщҫЭПа№ШЧКБПөГіцЛьГЗУлН¶ИлЧКҪр![]() ЈЁНтФӘЈ©өДКэҫЭ·ЦұрИзПВұнәННјЛщКҫЈәЖдЦРТСЦӘјЧөДАыИуДЈРНОӘ
ЈЁНтФӘЈ©өДКэҫЭ·ЦұрИзПВұнәННјЛщКҫЈәЖдЦРТСЦӘјЧөДАыИуДЈРНОӘ![]() Ј¬ТТөДАыИуДЈРНОӘ
Ј¬ТТөДАыИуДЈРНОӘ![]() Ј®ЈЁ
Ј®ЈЁ![]() ОӘІОКэЈ¬ЗТ
ОӘІОКэЈ¬ЗТ![]() Ј©.
Ј©.
|
|
|
|
|
|
|
|
|
|

ЈЁ1Ј©ЗлёщҫЭПВұнУлНјЦРКэҫЭЈ¬·ЦұрЗуіцјЧЎўТТБҪЦЦІъЖ·ЛщөГөДАыИуУлН¶ИлЧКҪр![]() ЈЁНтФӘЈ©өДәҜКэДЈРН
ЈЁНтФӘЈ©өДәҜКэДЈРН
ЈЁ2Ј©ҪсҪ«![]() НтЧКҪрН¶ИлЙъІъјЧЎўТТБҪЦЦІъЖ·Ј¬ІўТӘЗу¶ФјЧЎўТТБҪЦЦІъЖ·өДН¶ИлЧКҪр¶јІ»өНУЪ
НтЧКҪрН¶ИлЙъІъјЧЎўТТБҪЦЦІъЖ·Ј¬ІўТӘЗу¶ФјЧЎўТТБҪЦЦІъЖ·өДН¶ИлЧКҪр¶јІ»өНУЪ![]() НтФӘЈ®Йи¶ФТТЦЦІъЖ·Н¶ИлЧКҪр
НтФӘЈ®Йи¶ФТТЦЦІъЖ·Н¶ИлЧКҪр![]() ЈЁНтФӘЈ©Ј¬ІўЙиЧЬАыИуОӘ
ЈЁНтФӘЈ©Ј¬ІўЙиЧЬАыИуОӘ![]() ЈЁНтФӘЈ©Ј¬ИзәО·ЦЕдН¶ИлЧКҪрЈ¬ІЕДЬК№ЧЬАыИуЧоҙуЈҝІўЗуіцЧоҙуЧЬАыИуЈ®
ЈЁНтФӘЈ©Ј¬ИзәО·ЦЕдН¶ИлЧКҪрЈ¬ІЕДЬК№ЧЬАыИуЧоҙуЈҝІўЗуіцЧоҙуЧЬАыИуЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»
Ј»![]() ЈЁ2Ј©өұјЧІъЖ·Н¶Ил
ЈЁ2Ј©өұјЧІъЖ·Н¶Ил![]() НтФӘЈ¬ТТІъЖ·Н¶Ил
НтФӘЈ¬ТТІъЖ·Н¶Ил![]() НтФӘКұЈ¬ЧЬАыИуЧоҙуОӘ
НтФӘКұЈ¬ЧЬАыИуЧоҙуОӘ![]() НтФӘ
НтФӘ
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭМвТв,Ҫ«КэҫЭ·ЦұрҙъИлјЧЎўТТБҪЦЦІъЖ·ЛщөГөДАыИуУлН¶ИлЧКҪр![]() ЈЁНтФӘЈ©өДәҜКэДЈРНЦР,Ҫв·ҪіМЧй,јҙҝЙЗуіцәҜКэұнҙпКҪ.
ЈЁНтФӘЈ©өДәҜКэДЈРНЦР,Ҫв·ҪіМЧй,јҙҝЙЗуіцәҜКэұнҙпКҪ.
ЈЁ2Ј©ёщҫЭМвТв,Йи¶ФТТЦЦІъЖ·Н¶ЧК![]() ,¶ФјЧЦЦІъЖ·Н¶ЧК
,¶ФјЧЦЦІъЖ·Н¶ЧК![]() ,ҙъИлБҪёцАыИу№«КҪ,АыУГ»»ФӘ·ЁЗуіцәҜКэөДЦөУт,И»әуЗуЧоҙуЦөјҙҝЙ.
,ҙъИлБҪёцАыИу№«КҪ,АыУГ»»ФӘ·ЁЗуіцәҜКэөДЦөУт,И»әуЗуЧоҙуЦөјҙҝЙ.
ҪвЈәЈЁ1Ј©УЙјЧөДКэҫЭұнҪбәПДЈРН![]() ҙъИлБҪөгҝЙөГ
ҙъИлБҪөгҝЙөГ![]()
![]()
ҙъИлУР![]()
өГ![]() ,
,![]()
јҙ![]()
УЙТТөДКэҫЭНјҪбәПДЈРН![]() ҙъИлИэёцөгҝЙөГ
ҙъИлИэёцөгҝЙөГ![]() ,
,![]() ,
,![]() ҝЙөГ
ҝЙөГ
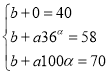 ,
,
өГ![]() ,
,![]() ,
,![]()
јҙ![]()
ЈЁ2Ј©ёщҫЭМвТв,¶ФТТЦЦІъЖ·Н¶ЧК![]() ЈЁНтФӘЈ©,¶ФјЧЦЦІъЖ·Н¶ЧК
ЈЁНтФӘЈ©,¶ФјЧЦЦІъЖ·Н¶ЧК![]() ЈЁНтФӘЈ©,
ЈЁНтФӘЈ©,
ДЗГҙЧЬАыИу![]()
![]() ,
,
УЙ![]() ,ҪвөГ
,ҪвөГ![]() ,
,
ЛщТФ![]() ,
,
Бо![]() ,
,![]() ,№К
,№К![]() ,
,
Фт![]()
![]() ,
,
ЛщТФөұ![]() Кұ,јҙ
Кұ,јҙ![]() Кұ,
Кұ,![]() ,
,
ҙрЈәөұјЧІъЖ·Н¶Ил![]() НтФӘ,ТТІъЖ·Н¶Ил
НтФӘ,ТТІъЖ·Н¶Ил![]() НтФӘКұ,ЧЬАыИуЧоҙуОӘ
НтФӘКұ,ЧЬАыИуЧоҙуОӘ![]() НтФӘ
НтФӘ



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ ҫЭ№ЫІвНіјЖЈ¬ДіКӘөШ№«Ф°ДіЦЦХдПЎДсАаөДПЦУРёцКэФј![]() Ц»Ј¬ІўТФЖҪҫщГҝДк
Ц»Ј¬ІўТФЖҪҫщГҝДк![]() өДЛЩ¶ИФцјУЈ®
өДЛЩ¶ИФцјУЈ®
(1)ЗуБҪДкәуХвЦЦХдПЎДсАаөДҙуФјёцКэЈ»
(2)Рҙіц![]() ЈЁХдПЎДсАаөДёцКэЈ©№ШУЪ
ЈЁХдПЎДсАаөДёцКэЈ©№ШУЪ![]() ЈЁҫӯ№эөДДкКэЈ©өДәҜКэ№ШПөКҪЈ»
ЈЁҫӯ№эөДДкКэЈ©өДәҜКэ№ШПөКҪЈ»
(3)Фјҫӯ№э¶аЙЩДкТФәуЈ¬ХвЦЦДсАаөДёцКэҙпөҪПЦУРёцКэөД![]() ұ¶»тТФЙПЈҝЈЁҪб№ыОӘХыКэЈ©(ІОҝјКэҫЭЈә
ұ¶»тТФЙПЈҝЈЁҪб№ыОӘХыКэЈ©(ІОҝјКэҫЭЈә![]() Ј¬
Ј¬![]() )
)
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬![]() КЗұЯіӨОӘ
КЗұЯіӨОӘ![]() өДХэ·ҪРОЈ¬
өДХэ·ҪРОЈ¬![]() КЗ
КЗ![]() өДЦРөгЈ¬өг
өДЦРөгЈ¬өг![]() СШЧЕВ·ҫ¶
СШЧЕВ·ҫ¶![]() ФЪХэ·ҪРОұЯЙПФЛ¶ҜЛщҫӯ№эөДВ·іМОӘ
ФЪХэ·ҪРОұЯЙПФЛ¶ҜЛщҫӯ№эөДВ·іМОӘ![]() Ј¬
Ј¬![]() өДГж»эОӘ
өДГж»эОӘ![]() .
.

ЈЁ1Ј©Зу![]() өДҪвОцКҪј°¶ЁТеУтЈ»
өДҪвОцКҪј°¶ЁТеУтЈ»
ЈЁ2Ј©Зу![]() Гж»эөДЧоҙуЦөј°ҙЛКұөг
Гж»эөДЧоҙуЦөј°ҙЛКұөг![]() О»ЦГ.
О»ЦГ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
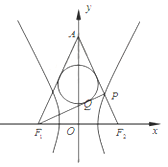
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЛ«ЗъПЯ![]() өДЧуУТҪ№өг·ЦұрОӘ
өДЧуУТҪ№өг·ЦұрОӘ![]() ,
,![]() Ј¬
Ј¬![]() КЗЛ«ЗъПЯУТЦ§ЙПөДТ»өгЈ¬
КЗЛ«ЗъПЯУТЦ§ЙПөДТ»өгЈ¬![]() Ул
Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() өДДЪЗРФІФЪұЯ
өДДЪЗРФІФЪұЯ![]() ЙПөДЗРөгОӘ
ЙПөДЗРөгОӘ![]() Ј¬Иф
Ј¬Иф![]() Ј¬ФтЛ«ЗъПЯөДАлРДВККЗ ( )
Ј¬ФтЛ«ЗъПЯөДАлРДВККЗ ( )
A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ ЗТөг
ЗТөг![]() ФЪәҜКэ
ФЪәҜКэ![]() өДНјПуЙПЈ®
өДНјПуЙПЈ®

ЈЁ1Ј©ЗуәҜКэ![]() өДҪвОцКҪЈ¬ІўФЪНјЦРөДЦұҪЗЧшұкПөЦР»ӯіцәҜКэ
өДҪвОцКҪЈ¬ІўФЪНјЦРөДЦұҪЗЧшұкПөЦР»ӯіцәҜКэ![]() өДНјПуЈ»
өДНјПуЈ»
ЈЁ2Ј©ЗуІ»өИКҪ![]() өДҪвјҜЈ»
өДҪвјҜЈ»
ЈЁ3Ј©Иф·ҪіМ![]() УРБҪёцІ»ПаөИөДКөКэёщЈ¬ЗуКөКэ
УРБҪёцІ»ПаөИөДКөКэёщЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЦұИэАвЦщ![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() .
.

ЈЁ1Ј©Иф![]() Ј¬ЗуЦұПЯ
Ј¬ЗуЦұПЯ![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙҪЗөДХэПТЦөЈ»
ЛщіЙҪЗөДХэПТЦөЈ»
ЈЁ2Ј©Иф¶юГжҪЗ![]() өДҙуРЎОӘ
өДҙуРЎОӘ![]() Ј¬ЗуКөКэ
Ј¬ЗуКөКэ![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЛ«ЗъПЯx2Јӯ![]() ЈҪ1.
ЈҪ1.
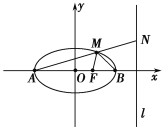
(1)ИфТ»НЦФІУлёГЛ«ЗъПЯ№ІҪ№өгЈ¬ЗТУРТ»Ҫ»өгP(2,3)Ј¬ЗуНЦФІ·ҪіМЈ®
(2)Йи(1)ЦРНЦФІөДЧуЎўУТ¶Ҙөг·ЦұрОӘAЎўBЈ¬УТҪ№өгОӘFЈ¬ЦұПЯlОӘНЦФІөДУТЧјПЯЈ¬NОӘlЙПөДТ»¶ҜөгЈ¬ЗТФЪxЦбЙП·ҪЈ¬ЦұПЯANУлНЦФІҪ»УЪөгM.ИфAMЈҪMNЈ¬ЗуЎПAMBөДУаПТЦөЈ»
(3)Йи№эAЎўFЎўNИэөгөДФІУлyЦбҪ»УЪPЎўQБҪөгЈ¬өұПЯ¶ОPQөДЦРөгОӘ(0,9)КұЈ¬ЗуХвёцФІөД·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ![]() Ј¬
Ј¬![]() ·ЦұрКЗЛ«ЗъПЯ
·ЦұрКЗЛ«ЗъПЯ![]() өДЧу¶ҘөгЎўУТҪ№өгЈ¬№э
өДЧу¶ҘөгЎўУТҪ№өгЈ¬№э![]() өДЦұПЯ
өДЦұПЯ![]() Ул
Ул![]() өДТ»МхҪҘҪьПЯҙ№ЦұЗТУлБнТ»МхҪҘҪьПЯәН
өДТ»МхҪҘҪьПЯҙ№ЦұЗТУлБнТ»МхҪҘҪьПЯәН![]() Цб·ЦұрҪ»УЪ
Цб·ЦұрҪ»УЪ![]() Ј¬
Ј¬![]() БҪөг.Иф
БҪөг.Иф![]() Ј¬Фт
Ј¬Фт![]() өДАлРДВККЗЈЁ Ј©
өДАлРДВККЗЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙи№ШУЪxөД·ҪіМ2x2©Ғax©Ғ2=0өДБҪёщ·ЦұрОӘҰБЎўҰВЈЁҰБЈјҰВЈ©Ј¬әҜКэ![]()
ЈЁ1Ј©ЦӨГчfЈЁxЈ©ФЪЗшјдЈЁҰБЈ¬ҰВЈ©ЙПКЗФцәҜКэЈ»
ЈЁ2Ј©өұaОӘәОЦөКұЈ¬fЈЁxЈ©ФЪЗшјд[ҰБЈ¬ҰВ]ЙПөДЧоҙуЦөУлЧоРЎЦөЦ®ІоЧоРЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com