[题目]过点C(3,4)且与轴.轴都相切的两个圆的半径分别为.则= ．题目和参考答案——青夏教育精英家教网—

【题目】过点C(3,4)且与轴，轴都相切的两个圆的半径分别为，则=______．

【答案】25

【解析】

满足与x轴，y轴都相切的圆的圆心在第一象限，设出圆心（a，a），根据切线的性质得到半径r=a，表示出圆的标准方程，由C在此圆上，将C的坐标代入圆的方程中，得到关于a的一元二次方程，根据r1，r2为此一元二次方程的两个解，利用根与系数的关系即可得出r1r2的值．

由题意得：满足与x轴，y轴都相切的圆的圆心在第一象限，设圆心坐标为（a，a），则半径r=a，∴圆的方程为（x﹣a）2+（y﹣a）2=a2，又C（3，4）在此圆上，

∴将C的坐标代入得：（3﹣a）2+（4﹣a）2=a2，整理得：a2﹣14a+25=0，

∵r1，r2分别为a2﹣14a+25=0的两个解，∴r1r2=25．

故答案为：25

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面是菱形，，平面，，点分别为和中点.

（1）求证：直线平面；

（2）求证：面；

（3）求与平面所成角的正弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了让学生更多的了解“数学史”知识，梁才学校高二年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有800名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，统计结果见下表．请你根据频率分布表解答下列问题：

序号	分组	组中值	频数	频率
（i）	（分数）	（Gi）	（人数）	（Fi）
1		65	①	0.12
2		75	20	②
3		85	③	0.24
4		95	④	⑤
合计			50	1

（1）填充频率分布表中的空格；

（2）为鼓励更多的学生了解“数学史”知识，成绩不低于85分的同学能获奖，请估计在

参加的800名学生中大概有多少名学生获奖？（3）在上述统计数据的分析中有一项计算见算法流程图，求输出的S的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线y= x2的焦点，离心率等于．
（1）求椭圆C的方程；
（2）过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若 =λ1 ，，求证：λ1+λ2为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(1)求与双曲线有相同的焦点且过点的双曲线标准方程；

(2)求焦点在直线上的抛物线的标准方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】进入冬季以来，我国北方地区的雾霾天气持续出现，极大的影响了人们的健康和出行，我市环保局对该市2015年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的空气质量指数频率分布直方图，如图．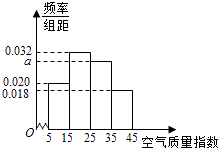

（1）求a的值；
（2）如果空气质量指数不超过15，就认定空气质量为“特优等级”，则从今年的监测数据中随机抽取3天的数值，其中达到“特优等级”的天数为X．求X的分布列和数学期望．