
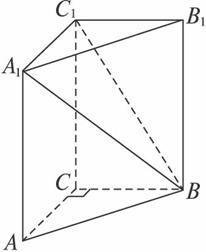
图4
(文)如图5,在正四棱锥P—ABCD中,PA=2,直线PA与平面ABCD所成的角为60°,求正四棱锥P—ABCD的体积V.
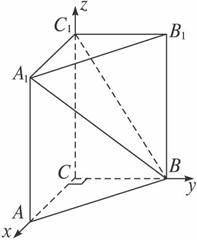
图5
答案:(理)解法一:由题意,可得体积V=CC1·S△ABC=CC1·![]() ·AC·BC=
·AC·BC=![]() CC1=1,
CC1=1,
∴AA1=CC1=2.

连结BC1.∵A1C1⊥B1C1,A1C1⊥CC1,∴A1C1⊥平面BB1C1C.
∴∠A1BC1是直线A1B与平面BB1C1C所成的角.
BC1=![]() ,
,
∴tan∠A1BC1=![]() ,则∠A1BC1=arctan
,则∠A1BC1=arctan![]() .
.
故直线A1B与平面BB1C1C所成角的大小为arctan![]() .
.
解法二:由题意,可得体积V=CC1·S△ABC=CC1·![]() ·AC·BC=
·AC·BC=![]() CC1=1,∴CC1=2.
CC1=1,∴CC1=2.
如图,建立空间直角坐标系,得点B(0,1,0),C1(0,0,2),A1(1,0,2),

则![]() =(-1,1,-2),平面BB1C1C的法向量为n=(1,0,0).
=(-1,1,-2),平面BB1C1C的法向量为n=(1,0,0).
设直线A1B与平面BB1C1C所成的角为θ,![]() 与n的夹角为φ,
与n的夹角为φ,
则cosφ=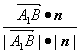 =-
=-![]() ,
,
∴sinθ=|cosφ|=![]() ,θ=arcsin
,θ=arcsin![]() .
.
故直线A1B与平面BB1C1C所成角的大小为arcsin![]() .
.
(文)解:作PO⊥平面ABCD,垂足为O.连结AO,O是正方形ABCD的中心,∠PAO是直线PA与平面ABCD所成的角.
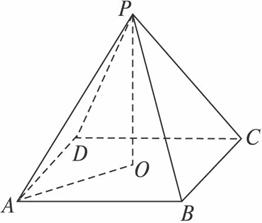
∠PAO=60°,PA=2,∴PO=![]() ,AO=1,AB=
,AO=1,AB=![]() .∴V=
.∴V=![]() PO·SABCD=
PO·SABCD=![]() ×
×![]() ×2=
×2=![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:四川省树德协进中学2011-2012学年高二上学期期中考试数学试题 题型:022
(理)如图,正△ABC的中线AF与中位线DE相交于G,已知△![]() ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
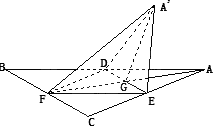
(1)动点![]() 在平面ABC上的射影在线段AF上;
在平面ABC上的射影在线段AF上;
(2)恒有平面![]() GF⊥平面BCED;
GF⊥平面BCED;
(3)三棱锥![]() -FED的体积有最大值;
-FED的体积有最大值;
(4)异面直线![]() E与BD不可能垂直.
E与BD不可能垂直.
其中正确的命题的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区二模理)如图,在体积为V1的正方体ABCD―A1B1C1D1中,M,N分别
为所在边的中点,正方体的外接球的体积为V,有如下四个命题;
①BD1=![]()
②BD1与底面ABCD所成角是45°;
③![]() ;
;
④MN//平面D1BC。其中正确命题的个数为( )
A.4 B.3
C.2 D.1

查看答案和解析>>
科目:高中数学 来源: 题型:
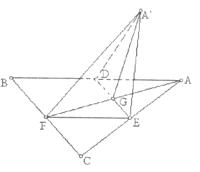
(08年杭州市质检二理) 如图,边长为![]() 的正
的正![]() 中线
中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号)。
旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号)。
(1)动点![]() 在平面
在平面![]() 上的射影是线段
上的射影是线段![]()
(2)三棱锥![]() 的体积有最大值;
的体积有最大值;
(3)恒有平面![]() 平面
平面![]() ;
;
(4)异面直线![]() 与
与![]() 不可能互相垂直;
不可能互相垂直;
(5)异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
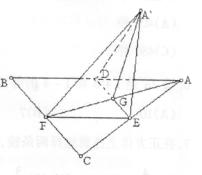
(08年金华一中理) 如图,边长为![]() 的正
的正![]() 中线
中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (填上所有正确命题的序号)。
旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (填上所有正确命题的序号)。
(1)动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上;
上;
(2)三棱锥![]() 的体积有最大值;
的体积有最大值;
(3)恒有平面![]() 平面
平面![]() ;
;
(4)异面直线![]() 与
与![]() 不可能互相垂直;
不可能互相垂直;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com