
ΓΨΧβΡΩΓΩΤΫΕΞ…Ϋ –ΙΪΑ≤Ψ÷ΫΜΨ·÷ßΕ”“άΨίΓΕ÷–ΜΣ»ΥΟώΙ≤ΚΆΙζΒά¬ΖΫΜΆ®Α≤»ΪΖ®ΓΖΒΎ![]() ΧθΙφΕ®ΘΚΥυ”–÷ςΗ…Βά¬ΖΖ≤ΜζΕ·≥ΒΆΨΨ≠ °Ή÷ΩΎΜρΑΏ¬μœΏΘ§Έό¬έΉΣΆδΜρ’Ώ÷±––Θ§”ω”–––»ΥΙΐ¬μ¬ΖΘ§±Ί–κάώ»Ο––»ΥΘ§ΈΞΖ¥’ΏΫΪ±Μ¥Π“‘
ΧθΙφΕ®ΘΚΥυ”–÷ςΗ…Βά¬ΖΖ≤ΜζΕ·≥ΒΆΨΨ≠ °Ή÷ΩΎΜρΑΏ¬μœΏΘ§Έό¬έΉΣΆδΜρ’Ώ÷±––Θ§”ω”–––»ΥΙΐ¬μ¬ΖΘ§±Ί–κάώ»Ο––»ΥΘ§ΈΞΖ¥’ΏΫΪ±Μ¥Π“‘![]() ‘ΣΖΘΩνΘ§Φ«
‘ΣΖΘΩνΘ§Φ«![]() Ζ÷ΒΡ––’ΰ¥ΠΖΘΘ°»γ±μ «±Ψ –“Μ÷ςΗ…¬ΖΕΈΦύΩΊ…η±ΗΥυΉΞ≈ΡΒΡ
Ζ÷ΒΡ––’ΰ¥ΠΖΘΘ°»γ±μ «±Ψ –“Μ÷ςΗ…¬ΖΕΈΦύΩΊ…η±ΗΥυΉΞ≈ΡΒΡ![]() Ηω‘¬ΡΎΘ§ΜζΕ·≥ΒΦί Μ‘±≤ΜΓΑάώ»ΟΑΏ¬μœΏΓ±––ΈΣΆ≥ΦΤ ΐΨίΘΚ
Ηω‘¬ΡΎΘ§ΜζΕ·≥ΒΦί Μ‘±≤ΜΓΑάώ»ΟΑΏ¬μœΏΓ±––ΈΣΆ≥ΦΤ ΐΨίΘΚ
‘¬Ζί |
|
|
|
|
|
ΈΞ’¬Φί Μ‘±»Υ ΐ |
|
|
|
|
|
Θ®ΔώΘ©«κάϊ”ΟΥυΗχ ΐΨί«σΈΞ’¬»Υ ΐ![]() ”ꑬΖί
”ꑬΖί![]() ÷°ΦδΒΡΜΊΙι÷±œΏΖΫ≥Χ
÷°ΦδΒΡΜΊΙι÷±œΏΖΫ≥Χ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©‘Λ≤βΗΟ¬ΖΕΈ![]() ‘¬ΖίΒΡ≤ΜΓΑάώ»ΟΑΏ¬μœΏΓ±ΈΞ’¬Φί Μ‘±»Υ ΐΘ°
‘¬ΖίΒΡ≤ΜΓΑάώ»ΟΑΏ¬μœΏΓ±ΈΞ’¬Φί Μ‘±»Υ ΐΘ°
≤ΈΩΦΙΪ ΫΘΚ Θ§
Θ§![]() Θ°
Θ°
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕP©¹ABCD÷–Θ§ADΓΆΤΫΟφPABΘ§APΓΆABΘ° 
Θ®1Θ©«σ÷ΛΘΚCDΓΆAPΘΜ
Θ®2Θ©»τCDΓΆPDΘ§«σ÷ΛΘΚCDΓΈΤΫΟφPABΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪ±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–Έ![]() ―ΊΕ‘Ϋ«œΏ
―ΊΕ‘Ϋ«œΏ![]() ’έΤπΘ§ ΙΒΟΤΫΟφ
’έΤπΘ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§‘Ύ’έΤπΚσ–Έ≥…ΒΡ»ΐάβΉΕ
Θ§‘Ύ’έΤπΚσ–Έ≥…ΒΡ»ΐάβΉΕ![]() ÷–Θ§Ηχ≥ωœ¬Ν–ΥΡ÷÷ΥΒΖ®ΘΚ
÷–Θ§Ηχ≥ωœ¬Ν–ΥΡ÷÷ΥΒΖ®ΘΚ
ΔΌ![]() «Β»±Ώ»ΐΫ«–ΈΘΜΔΎ
«Β»±Ώ»ΐΫ«–ΈΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔή÷±œΏ
ΘΜΔή÷±œΏ![]() ΚΆ
ΚΆ![]() Υυ≥…ΒΡΫ«ΒΡ¥σ–ΓΈΣ
Υυ≥…ΒΡΫ«ΒΡ¥σ–ΓΈΣ![]() Θ°Τδ÷–Υυ”–’ΐ»ΖΒΡ–ρΚ≈ «Θ® Θ©
Θ°Τδ÷–Υυ”–’ΐ»ΖΒΡ–ρΚ≈ «Θ® Θ©

A. ΔΌΔέB. ΔΎΔήC. ΔΌΔΎΔέD. ΔΌΔΎΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΌΕ®Ρ≥…δ ÷…δΜς“Μ¥ΈΟϋ÷–ΡΩ±ξΒΡΗ≈¬ ΈΣ![]() Θ°œ÷”–4ΖΔΉ”Β·Θ§ΗΟ…δ ÷“ΜΒ©…δ÷–ΡΩ±ξΘ§ΨΆΆΘ÷Ι…δΜςΘ§Ζώ‘ρΨΆ“Μ÷±ΕάΝΔΒΊ…δΜςΒΫΉ”Β·”ΟΆξΘ°…ηΚΡ”ΟΉ”Β· ΐΈΣXΘ§«σΘΚ
Θ°œ÷”–4ΖΔΉ”Β·Θ§ΗΟ…δ ÷“ΜΒ©…δ÷–ΡΩ±ξΘ§ΨΆΆΘ÷Ι…δΜςΘ§Ζώ‘ρΨΆ“Μ÷±ΕάΝΔΒΊ…δΜςΒΫΉ”Β·”ΟΆξΘ°…ηΚΡ”ΟΉ”Β· ΐΈΣXΘ§«σΘΚ
Θ®1Θ©XΒΡΗ≈¬ Ζ÷≤ΦΘΜ
Θ®2Θ© ΐ―ßΤΎΆϊE(X)Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©»τ![]() Θ§
Θ§ ![]() ΕΦ «¥”0Θ§1Θ§2Θ§3Θ§4ΈεΗω ΐ÷–»Έ»ΓΒΡ“ΜΗω ΐΘ§«σ…œ ωΚ· ΐ”–ΝψΒψΒΡΗ≈¬ ΘΜ
ΕΦ «¥”0Θ§1Θ§2Θ§3Θ§4ΈεΗω ΐ÷–»Έ»ΓΒΡ“ΜΗω ΐΘ§«σ…œ ωΚ· ΐ”–ΝψΒψΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τ![]() Θ§
Θ§ ![]() ΕΦ «¥”«χΦδ
ΕΦ «¥”«χΦδ![]() …œ»Έ»ΓΒΡ“ΜΗω ΐΘ§«σ
…œ»Έ»ΓΒΡ“ΜΗω ΐΘ§«σ![]() ≥…ΝΔΒΡΗ≈¬ .
≥…ΝΔΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ»γΆΦΥυ ΨΒΡΦΗΚΈΧε÷–Θ§ΥΡ±Ώ–Έ![]() «’ΐΖΫ–ΈΘ§
«’ΐΖΫ–ΈΘ§ ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§ ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΒΡ÷–ΒψΘ§«“
ΒΡ÷–ΒψΘ§«“![]() .
.
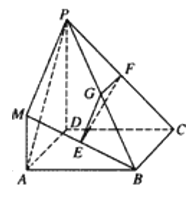
Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷ΛΘΚΤΫΟφP![]() ΘΜ
ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±ΥΡάβ÷υABCD©¹A1B1C1D1÷–Θ§ΒΉΟφΥΡ±Ώ–ΈABCDΈΣΝβ–ΈΘ§A1A=AB=2Θ§ΓœABC= ![]() Θ§EΘ§FΖ÷±π «BCΘ§A1CΒΡ÷–ΒψΘ°
Θ§EΘ§FΖ÷±π «BCΘ§A1CΒΡ÷–ΒψΘ° 
Θ®1Θ©«σ“λΟφ÷±œΏEFΘ§ADΥυ≥…Ϋ«ΒΡ”ύœ“÷ΒΘΜ
Θ®2Θ©ΒψM‘ΎœΏΕΈA1D…œΘ§ ![]() =ΠΥΘ°»τCMΓΈΤΫΟφAEFΘ§«σ Β ΐΠΥΒΡ÷ΒΘ°
=ΠΥΘ°»τCMΓΈΤΫΟφAEFΘ§«σ Β ΐΠΥΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –Βγ ”Χ®ΈΣΝΥ–ϊ¥ΪΨΌΑλΈ ¥πΜνΕ·Θ§ΥφΜζΕ‘ΗΟ –15ΓΪ65ΥξΒΡ»Υ»Κ≥ι―υΝΥ![]() »ΥΘ§ΜΊ¥πΈ ΧβΦΤΫαΙϊ»γœ¬ΆΦ±μΥυ ΨΘΚ
»ΥΘ§ΜΊ¥πΈ ΧβΦΤΫαΙϊ»γœ¬ΆΦ±μΥυ ΨΘΚ

Θ®1Θ©Ζ÷±π«σ≥ω![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©¥”ΒΎ2Θ§3Θ§4ΉιΜΊ¥π’ΐ»ΖΒΡ»Υ÷–”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ6»ΥΘ§‘ρΒΎ2Θ§3Θ§4ΉιΟΩΉιΗς≥ι»ΓΕύ…Ό»ΥΘΩ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡ«ΑΧαœ¬Θ§Βγ ”Χ®ΨωΕ®‘ΎΥυ≥ι»ΓΒΡ6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΑδΖΔ–“‘ΥΫ±Θ§«σΥυ≥ι»ΓΒΡ»Υ÷–ΒΎ2Ήι÷Ν…Ό”–1»ΥΜώΒΟ–“‘ΥΫ±ΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Υυ ΨΘ§‘ΎΒ»―ϋΧί–Έ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§¥ΙΉψΈΣ
Θ§¥ΙΉψΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°ΫΪ
Θ°ΫΪ![]() ―Ί
―Ί![]() ’έΤπΒΫ
’έΤπΒΫ![]() ΒΡΈΜ÷ΟΘ§ ΙΤΫΟφ
ΒΡΈΜ÷ΟΘ§ ΙΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§»γΆΦ2Υυ ΨΘ§Βψ
Θ§»γΆΦ2Υυ ΨΘ§Βψ![]() ΈΣάβ
ΈΣάβ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°

Θ®1Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®3Θ©«σ»ΐάβΉΕ![]() ΒΡΧεΜΐΘ°
ΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com