
 与
与
 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 处的切线平行,求实数
处的切线平行,求实数 的值;
的值; 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 取
取 最大值的
最大值的 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数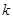 的值
的值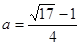 (2)
(2) 的最大值为
的最大值为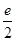 (3)
(3)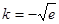
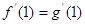 ,从而建立关于a的方程,解出a的值.
,从而建立关于a的方程,解出a的值.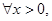
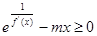 恒成立,转化为
恒成立,转化为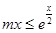 ,即
,即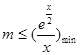 ,
, ,利用导数求其最小值即可.
,利用导数求其最小值即可.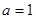 ,
,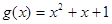 在
在 上的最小值
上的最小值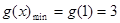 ,从而确定出
,从而确定出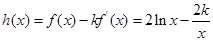 在
在 的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值
的最小值为3.下面再利用导数研究h(x)的最小值,根据最小值为3建立关于k的方程求出k的值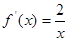 ,
,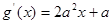 ,曲线
,曲线 和
和 在点
在点 处的切线平行,故
处的切线平行,故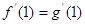 可得:
可得: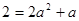 且
且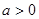 解得:
解得: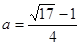 ---3分
---3分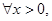
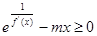 恒成立,即
恒成立,即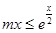 ,即
,即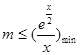 ,---4分
,---4分 ,
,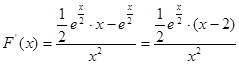 ,---5分
,---5分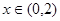 时,
时,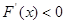 ,
,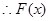 在
在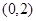 上单调递减
上单调递减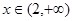 时,
时,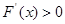 ,
,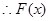 在
在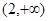 上单调递增 ---7分
上单调递增 ---7分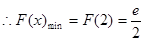 ,故
,故 的最大值为
的最大值为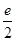 ---8分
---8分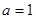 ,故
,故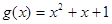 在
在 时,
时,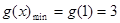
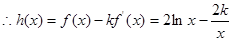 在
在 的最小值为3,
的最小值为3,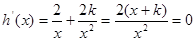 ,解得:
,解得: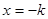 ---10分
---10分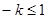 即
即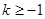 时,
时,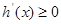 ,此时
,此时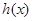 在
在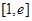 上单调递增
上单调递增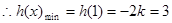 ,解得:
,解得: (不合前提) ---11分
(不合前提) ---11分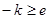 即
即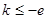 时,
时,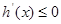 ,此时
,此时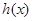 在
在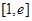 上单调递减
上单调递减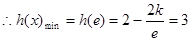 ,解得:
,解得: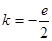 (不合前提)---12分
(不合前提)---12分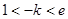 即
即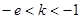 时,
时,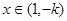 时,
时,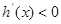 ,
,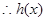 在
在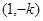 单调递减
单调递减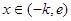 时,
时,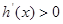 ,
,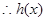 在
在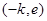 单调递增
单调递增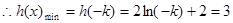 ,解得:
,解得: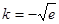 满足前提
满足前提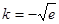


科目:高中数学 来源:不详 题型:填空题
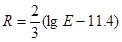 . 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;
. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且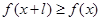 ,则称
,则称 为
为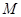 上的
上的 高调函数。如果定义域为
高调函数。如果定义域为 的函数
的函数 是奇函数,当
是奇函数,当 时,
时,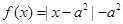 ,且
,且 为
为 上的4高调函数,那么实数
上的4高调函数,那么实数 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com