
°æƒø°øŒ™Ã·∏þ≤˙∆∑÷ ¡ø£¨ƒ≥∆Û“µ÷ ¡øπпÌ≤ø√≈æ≠≥£≤ª∂®∆⁄µÿ≥È≤È≤˙∆∑Ω¯––ºÏ≤‚£¨œ÷‘⁄ƒ≥Ãı…˙≤˙œþ…œÀʪ˙≥È»°100∏ˆ≤˙∆∑Ω¯––œýπÿ ˝æðµƒ∂‘±»£¨≤¢∂‘√ø∏ˆ≤˙∆∑Ω¯––◊€∫œ∆¿∑÷£®¬˙∑÷100∑÷£©£¨Ω´√ø∏ˆ≤˙∆∑À˘µ√µƒ◊€∫œ∆¿∑÷÷∆≥…»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº.º«◊€∫œ∆¿∑÷Œ™80∑÷º∞“‘…œµƒ≤˙∆∑Œ™“ªµ»∆∑.
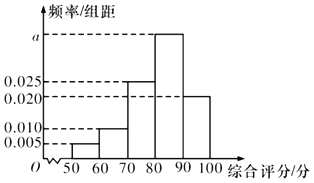
£®1£©«ÛÕº÷–![]() µƒ÷µ£¨≤¢«Û◊€∫œ∆¿∑÷µƒ÷–Œª ˝£ª
µƒ÷µ£¨≤¢«Û◊€∫œ∆¿∑÷µƒ÷–Œª ˝£ª
£®2£©”√—˘±æπ¿º∆◊Ð㨓‘∆µ¬ ◊˜Œ™∏≈¬ £¨∞¥∑÷≤„≥È—˘µƒÀºœÎ£¨œ»‘⁄∏√Ãı…˙≤˙œþ÷–Àʪ˙≥È»°5∏ˆ≤˙∆∑£¨‘Ÿ¥”’‚5∏ˆ≤˙∆∑÷–Àʪ˙≥È»°2∏ˆ≤˙∆∑º«¬º”–πÿ ˝æ𣨫ے‚2∏ˆ≤˙∆∑÷–«°”–“ª∏ˆ“ªµ»∆∑µƒ∏≈¬ .
°æ¥∞∏°ø(1) ![]() £ª÷–Œª ˝Œ™82.5. (2)
£ª÷–Œª ˝Œ™82.5. (2) ![]()
°æΩ‚Œˆ°ø
£®1£©∏˘æð∆µ¬ ÷Æ∫ÕŒ™1£¨Ω·∫œ∆µ¬ ∑÷≤º÷±∑ΩÕº∂‘”¶æÿ–Œ«¯”Ú√ʪ˝«ÛΩ‚º¥ø…£ªœ»Ω·∫œ ˝÷µ‘§≈–÷–Œª ˝À˘‘⁄◊Èæý”¶‘⁄80µΩ90÷ƺ‰£¨…Ë◊€∫œ∆¿∑÷µƒ÷–Œª ˝Œ™![]() £¨Ω·∫œ∆µ¬ º∆À„π´ Ω«ÛΩ‚º¥ø…£ª
£¨Ω·∫œ∆µ¬ º∆À„π´ Ω«ÛΩ‚º¥ø…£ª
£®2£©œ»Ω·∫œ∑÷≤„≥È—˘º∆À„≥ˆ“ªµ»∆∑À˘’º±»¿˝£¨‘Ÿ≤…”√¡–æŸ∑®±Ì æ≥ˆÀ˘”–ª˘±æ ¬º˛£¨Ω·∫œπ≈µ‰∏≈¬ π´ Ω«ÛΩ‚º¥ø…
£®1£©”…∆µ¬ ∫ÕŒ™1£¨µ√![]() £¨
£¨![]() £ª
£ª
…Ë◊€∫œ∆¿∑÷µƒ÷–Œª ˝Œ™![]() £¨‘Ú
£¨‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
À˘“‘◊€∫œ∆¿∑÷µƒ÷–Œª ˝Œ™82.5.
£®2£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷™£¨“ªµ»∆∑µƒ∆µ¬ Œ™![]() £¨º¥∏≈¬ Œ™0.6£ª
£¨º¥∏≈¬ Œ™0.6£ª
À˘“‘100∏ˆ≤˙∆∑÷–“ªµ»∆∑”–60∏ˆ£¨∑«“ªµ»∆∑”–40∏ˆ£¨‘Ú“ªµ»∆∑”Î∑«“ªµ»∆∑µƒ≥È—˘±»Œ™3£∫2£ª
À˘“‘œ÷≥È»°5∏ˆ≤˙∆∑£¨“ªµ»∆∑”–3∏ˆ£¨º«Œ™![]() °¢
°¢![]() °¢
°¢![]() £¨∑«“ªµ»∆∑2∏ˆ£¨º«Œ™
£¨∑«“ªµ»∆∑2∏ˆ£¨º«Œ™![]() °¢
°¢![]() £ª
£ª
¥”’‚5∏ˆ≤˙∆∑÷–Àʪ˙≥È»°2∏ˆ£¨ª˘±æ ¬º˛Œ™£∫![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() π≤10÷÷£ª
π≤10÷÷£ª
≥È»°µƒ’‚2∏ˆ≤˙∆∑÷–«°”–“ª∏ˆ“ªµ»∆∑µƒ ¬º˛Œ™£∫![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() π≤6÷÷£¨
π≤6÷÷£¨
À˘“‘À˘«Ûµƒ∏≈¬ Œ™![]() .
.


 ÃÏÃÏ¡∑ø⁄À„œµ¡–¥∞∏
ÃÏÃÏ¡∑ø⁄À„œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∏¥ ˝![]() ”Î∏¥∆Ω√Ê…œµ„
”Î∏¥∆Ω√Ê…œµ„![]() ∂‘”¶.
∂‘”¶.
£®1£©»Ù![]() «πÿ”⁄
«πÿ”⁄![]() µƒ“ª‘™∂˛¥Œ∑Ω≥Ã
µƒ“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒ“ª∏ˆ–È∏˘£¨«“
µƒ“ª∏ˆ–È∏˘£¨«“![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©…Ë∏¥ ˝![]() ¬˙◊„Ãıº˛
¬˙◊„Ãıº˛![]() £®∆‰÷–
£®∆‰÷–![]() °¢≥£ ˝
°¢≥£ ˝![]() £©£¨µ±
£©£¨µ±![]() Œ™∆Ê ˝ ±£¨∂ص„
Œ™∆Ê ˝ ±£¨∂ص„![]() µƒπϺ£Œ™
µƒπϺ£Œ™![]() £¨µ±
£¨µ±![]() Œ™≈º ˝ ±£¨∂ص„
Œ™≈º ˝ ±£¨∂ص„![]() µƒπϺ£Œ™
µƒπϺ£Œ™![]() £¨«“¡ΩÃı«˙œþ∂ºæ≠π˝µ„
£¨«“¡ΩÃı«˙œþ∂ºæ≠π˝µ„![]() £¨«ÛπϺ£
£¨«ÛπϺ£![]() ”Î
”Î![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨πϺ£![]() …œ¥Ê‘⁄µ„
…œ¥Ê‘⁄µ„![]() £¨ πµ„
£¨ πµ„![]() ”ε„
”ε„![]() µƒ◊Ó–°æý¿Î≤ª–°”⁄
µƒ◊Ó–°æý¿Î≤ª–°”⁄![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø√¸Ã‚![]() £∫∑Ω≥Ã
£∫∑Ω≥Ã![]() ±Ì æΩ𵄑⁄
±Ì æΩ𵄑⁄![]() ÷·…œµƒÀ´«˙œþ£∫√¸Ã‚
÷·…œµƒÀ´«˙œþ£∫√¸Ã‚![]() £∫»Ù¥Ê‘⁄
£∫»Ù¥Ê‘⁄![]() £¨ πµ√
£¨ πµ√![]() ≥…¡¢.
≥…¡¢.
£®1£©»Áπ˚√¸Ã‚![]() «’Ê√¸Ã‚£¨«Û µ ˝
«’Ê√¸Ã‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©»Áπ˚°∞![]() °±Œ™ºŸ√¸Ã‚£¨°∞
°±Œ™ºŸ√¸Ã‚£¨°∞![]() °±Œ™’Ê√¸Ã‚£¨«Û µ ˝
°±Œ™’Ê√¸Ã‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë![]() £¨
£¨![]() «∫Ø ˝
«∫Ø ˝![]() µƒÕºœÛ…œ»Œ“‚¡Ωµ„£¨»Ù
µƒÕºœÛ…œ»Œ“‚¡Ωµ„£¨»Ù![]() Œ™
Œ™![]() £¨
£¨![]() µƒ÷–µ„£¨«“
µƒ÷–µ„£¨«“![]() µƒ∫·◊¯±ÍŒ™
µƒ∫·◊¯±ÍŒ™![]() £Æ
£Æ
£®1£©«Û![]() £ª
£ª
£®2£©»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() £ª
£ª
£®3£©“—÷™ ˝¡–![]() µƒÕ®œÓπ´ Ω
µƒÕ®œÓπ´ Ω![]() £®
£®![]() £¨
£¨![]() £©£¨ ˝¡–
£©£¨ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨»Ù≤ªµ» Ω
£¨»Ù≤ªµ» Ω![]() ∂‘»Œ“‚
∂‘»Œ“‚![]() ∫„≥…¡¢£¨«Û
∫„≥…¡¢£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ëf£®x£© «∂®“‘⁄ µ ˝ºØR…œµƒ∫Ø ˝£¨«“y=f£®x+1£© «≈º∫Ø ˝£¨µ±x°ð1 ±£¨f£®x£©=2x©Å1£¨‘Úf£®![]() £©£¨f£®
£©£¨f£®![]() £©£¨f£®
£©£¨f£®![]() £©µƒ¥Û–°πÿœµ «£®°°°°£©
£©µƒ¥Û–°πÿœµ «£®°°°°£©
A. f£®![]() £©£ºf£®
£©£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £© B. f£®
£© B. f£®![]() £©£ºf£®
£©£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©
£©
C. f£®![]() £©£ºf£®
£©£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £© D. f£®
£© D. f£®![]() £©£ºf£®
£©£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂Ø‘≤![]() π˝µ„
π˝µ„![]() «“”Î÷±œþ
«“”Î÷±œþ![]() œý«–£¨‘≤–ƒ
œý«–£¨‘≤–ƒ![]() µƒπϺ£Œ™«˙œþ
µƒπϺ£Œ™«˙œþ![]() .
.
£®1£©«Û«˙œþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©»Ù![]() £¨
£¨![]() ««˙œþ
««˙œþ![]() …œµƒ¡Ω∏ˆµ„«“÷±œþ
…œµƒ¡Ω∏ˆµ„«“÷±œþ![]() π˝
π˝![]() µƒÕ‚–ƒ£¨∆‰÷–
µƒÕ‚–ƒ£¨∆‰÷–![]() Œ™◊¯±Í‘≠µ„£¨«Û÷§£∫÷±œþ
Œ™◊¯±Í‘≠µ„£¨«Û÷§£∫÷±œþ![]() π˝∂®µ„.
π˝∂®µ„.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄’˝∑ΩÃÂ![]() ÷–£¨E°¢F°¢G°¢H∑÷± «¿‚
÷–£¨E°¢F°¢G°¢H∑÷± «¿‚![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() µƒ÷–µ„.
µƒ÷–µ„.
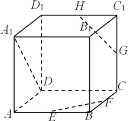
£®1£©≈–∂œ÷±œþ![]() ”Î
”Î![]() µƒŒª÷√πÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
µƒŒª÷√πÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©«Û“Ï√Ê÷±œþ![]() ”Î
”Î![]() À˘≥…µƒΩ«µƒ¥Û–°.
À˘≥…µƒΩ«µƒ¥Û–°.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë ˝¡–![]() µƒ«∞nœÓ∫ÕŒ™
µƒ«∞nœÓ∫ÕŒ™![]() £¨∂‘»Œ“‚µƒ’˝’˚ ˝n£¨∂º”–
£¨∂‘»Œ“‚µƒ’˝’˚ ˝n£¨∂º”–![]() ≥…¡¢£¨º«
≥…¡¢£¨º«![]() .
.
(1)«Û ˝¡–![]() ”Î ˝¡–
”Î ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
(2)«Û÷§£∫¢Ÿ![]() ∂‘
∂‘![]() ∫„≥…¡¢.¢⁄
∫„≥…¡¢.¢⁄![]() ∂‘
∂‘![]() ∫„≥…¡¢£¨∆‰÷–
∫„≥…¡¢£¨∆‰÷–![]() Œ™ ˝¡–
Œ™ ˝¡–![]() µƒ«∞nœÓ∫Õ.
µƒ«∞nœÓ∫Õ.
(3)º«![]() £¨
£¨![]() Œ™
Œ™![]() µƒ«∞nœÓ∫Õ£¨«Û÷§£∫∂‘»Œ“‚’˝’˚ ˝n£¨∂º”–
µƒ«∞nœÓ∫Õ£¨«Û÷§£∫∂‘»Œ“‚’˝’˚ ˝n£¨∂º”–![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ƒ≥–°«¯◊º±∏Ω´œ–÷√µƒ“ª÷±Ω«»˝Ω«–ŒµÿøÈø™∑¢≥…π´π≤¬Ãµÿ£¨Õº÷–![]() .…˺∆ ±“™«Û¬Ãµÿ≤ø∑÷£®»ÁÕº÷–“ı”∞≤ø∑÷À˘ 棩”–π´π≤¬Ãµÿ◊þµ¿
.…˺∆ ±“™«Û¬Ãµÿ≤ø∑÷£®»ÁÕº÷–“ı”∞≤ø∑÷À˘ 棩”–π´π≤¬Ãµÿ◊þµ¿![]() £¨«“¡Ω±þ «¡Ω∏ˆπÿ”⁄◊þµ¿
£¨«“¡Ω±þ «¡Ω∏ˆπÿ”⁄◊þµ¿![]() ∂‘≥∆µƒ»˝Ω«–Œ£®
∂‘≥∆µƒ»˝Ω«–Œ£®![]() ∫Õ
∫Õ![]() £©.œ÷øº¬«∑Ω±„∫լõÿ◊ӥ۪ؑ≠‘Ú£¨“™«Ûµ„
£©.œ÷øº¬«∑Ω±„∫լõÿ◊ӥ۪ؑ≠‘Ú£¨“™«Ûµ„![]() ”ε„
”ε„![]() æ˘≤ª÷ÿ∫œ£¨
æ˘≤ª÷ÿ∫œ£¨![]() ¬‰‘⁄±þ
¬‰‘⁄±þ![]() …œ«“≤ª”Î∂Àµ„
…œ«“≤ª”Î∂Àµ„![]() ÷ÿ∫œ£¨…Ë
÷ÿ∫œ£¨…Ë![]() .
.
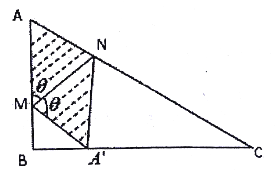
£®1£©»Ù![]() £¨«Û¥À ±π´π≤¬Ãµÿµƒ√ʪ˝£ª
£¨«Û¥À ±π´π≤¬Ãµÿµƒ√ʪ˝£ª
£®2£©Œ™∑Ω±„–°«¯æ”√Òµƒ––◊þ£¨…˺∆ ±“™«Û![]() µƒ≥§∂»◊Ó∂㨫ۥÀ ±¬Ãµÿπ´π≤◊þµ¿
µƒ≥§∂»◊Ó∂㨫ۥÀ ±¬Ãµÿπ´π≤◊þµ¿![]() µƒ≥§∂».
µƒ≥§∂».
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com