
 在平行四边形ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设
在平行四边形ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设 =
= ,
, =
= ,试用
,试用 、
、 表示
表示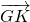 、
、 .
. 解:如图所示,因为AB、BC、CD的中点分别为E、F、G,
解:如图所示,因为AB、BC、CD的中点分别为E、F、G,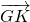 =
= +
+
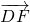 =
= +
+ (
(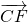 -
- )
)
 +
+ (-
(-
 +
+ )=-
)=-

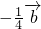 .(5分)
.(5分) =m
=m =m(
=m( +
+
 )=m
)=m +
+ m
m ;
;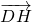 =n
=n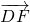 =n(
=n( -
- )=n
)=n -
- n
n .
. +
+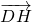 =
= ,所以
,所以 +n
+n =m
=m +
+
 (10分)
(10分) 解得m=
解得m= ,
, =
= (
( +
+ )=
)=
 +
+
 .(14分)
.(14分) 、
、 表示
表示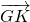 、
、 的目的,所研究的两个向量与两个基向量不在一个三角形中,故需要先用根据图形用与它们共线的向量将它们表示出来,然后再用两个基向量表示.
的目的,所研究的两个向量与两个基向量不在一个三角形中,故需要先用根据图形用与它们共线的向量将它们表示出来,然后再用两个基向量表示.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com