
【题目】如图,圆盘上有一指针,开始时指向圆盘的正上方.指针每次顺时针方向绕圆盘中心转动一角![]() ,且
,且![]() ,经2004次旋转,第一次回到了其初始位置,即又指向了圆盘的正上方.试问:
,经2004次旋转,第一次回到了其初始位置,即又指向了圆盘的正上方.试问:![]() 有多少个可能的不同值?
有多少个可能的不同值?

【答案】325
【解析】
显然有![]() .①
.①
这里![]() 是当指针第一次回到其初始位置时已经转过的圈数.
是当指针第一次回到其初始位置时已经转过的圈数.
因![]() 是正整数,式①整理后可得
是正整数,式①整理后可得![]() .
.
同时![]() 必与2004互质,即
必与2004互质,即![]() .
.
设![]() .若有
.若有![]() ,则令
,则令![]() .
.
此时有![]() .
.
这意味着指针转动![]() 次,每次转动角
次,每次转动角![]() ,指针则旋转
,指针则旋转![]() 圈之后,回到其初始位置,与题设矛盾.
圈之后,回到其初始位置,与题设矛盾.
由上述讨论可知,对任一满足![]() ,且
,且![]() 的
的![]() ,对应一个可能的
,对应一个可能的![]() .反之亦然.
.反之亦然.
故问题成为求满足上述两个条件的所有![]() 的个数.
的个数.
因为![]() ,
,
所以,![]() .
.
在不大于1001的正整数中,不能被2或3整除的正整数共有
![]() (个).
(个).
(符号![]() 表示不超过
表示不超过![]() 的最大整数.)
的最大整数.)
其中只有![]() 及
及![]() 能被167整除,所以,不大于1001且满足条件的
能被167整除,所以,不大于1001且满足条件的![]() 共有
共有![]() 个.再去掉1,5,7,11,13,17,19这7个不大于20的数,知同时满足两个条件的
个.再去掉1,5,7,11,13,17,19这7个不大于20的数,知同时满足两个条件的![]() 共有
共有![]() 个.
个.
因此,![]() 共有325个可能的不同值.
共有325个可能的不同值.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合).已知
是椭圆上一动点(与左、右顶点不重合).已知![]() 的面积的最大值为
的面积的最大值为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 、
、![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 a ∈ N+ , a ≥ 2 , 集合![]() .在闭区间[ 1, a ] 上是否存在 b , 使 A ∩ B ≠
.在闭区间[ 1, a ] 上是否存在 b , 使 A ∩ B ≠ ![]() ? 如果存在, 求出 b 的一切可能值及相应的 A ∩ B;如果不存在, 试说明理由.
? 如果存在, 求出 b 的一切可能值及相应的 A ∩ B;如果不存在, 试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,以![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为方程为
的极坐标方程为方程为![]() (
(![]() ),直线
),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)点![]() 在曲线
在曲线![]() 上,且曲线
上,且曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求点
垂直,求点![]() 的直角坐标和曲线C的参数方程;
的直角坐标和曲线C的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 有两个不同的交点,求直线
有两个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
span>女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
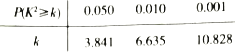 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com