
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
【答案】(1)见解析;(2)![]() 或
或![]() 或
或![]() ;(3)(0,1)∪(2,
;(3)(0,1)∪(2, ![]() ).
).
【解析】试题分析:(1)由递推关系,构造等比数列;(2)化简不等式得 ,依次验证m取1,2,3,4,即可得出;(3)分离参数,转化为求(2ak–ak+1)min即可.
,依次验证m取1,2,3,4,即可得出;(3)分离参数,转化为求(2ak–ak+1)min即可.
试题解析:
(1) 由an+1=![]() an+2,所以an+1–4 =
an+2,所以an+1–4 =![]() ( an–4 ),
( an–4 ),
且a1–4=–2,故数列{an–4}是以–2为首项,![]() 为公比的等比数列;
为公比的等比数列;
(2) 由(1)题,得an–4=–2![]() ,得
,得![]() ,
,
于是 ,当m≥4时,
,当m≥4时, ,无解,
,无解,
因此,满足题意的解为![]() 或
或![]() 或
或![]() ;
;
(3) 解:① 当k=1时,由![]() ,解得0<t<1或2<t<3,
,解得0<t<1或2<t<3,
② 当k≥2时,![]() ,故分母
,故分母![]() 恒成立,
恒成立,
从而,只需ak+1–t<2(ak–t)对k≥2,k∈N*恒成立,即t<2ak–ak+1对k≥2,k∈N*恒成立,故t<(2ak–ak+1)min,
又![]() ,故当
,故当![]() 时,
时,![]() ,所以
,所以![]() ,
,
综上所述,![]() 的取值范围是(0,1)∪(2,
的取值范围是(0,1)∪(2,![]() ).
).


科目:高中数学 来源: 题型:
【题目】一张坐标纸上涂着圆E: ![]() 及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
(1)求 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)直线 ![]() 与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若
与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若 ![]() ,求△ABO的面积的取值范围.
,求△ABO的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形SABC中,∠B=∠C= ![]() ,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 
(1)求证:PD⊥平面ABCD;
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
从本市随机抽取了10户家庭,统计了同一个月的用水量,得到如图所示的茎叶图.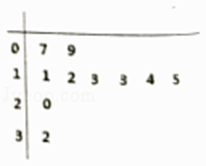
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( ) 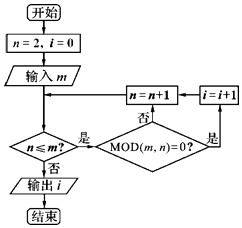
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (本小题满分12分)
已知圆C:![]() ,直线
,直线![]() 过定点A (1,0).
过定点A (1,0).
(1)若![]() 与圆C相切,求
与圆C相切,求![]() 的方程;
的方程;
(2)若![]() 与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线
与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于
,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于 ![]() 四点,四边形
四点,四边形 ![]() 的面积为
的面积为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]()
B.2
C.![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次数学考试后,某老师从甲,乙两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学成绩的中位数为73,则 ![]() 的值为( )
的值为( )
A.2
B.-2
C.3
D.-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com