
已知函数 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时, ,若函数在R上有且仅有4个零点,则a的取值范围是__________。
,若函数在R上有且仅有4个零点,则a的取值范围是__________。

解析试题分析:根据题意,由于函数 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时, ,那么可知当满足函数在R上有且仅有4个零点则可知
,那么可知当满足函数在R上有且仅有4个零点则可知 有四个不同的交点,只需要考虑在y轴右侧有两个交点即可,则可知,当相切时有一个,则此时的切点的斜率为a,即
有四个不同的交点,只需要考虑在y轴右侧有两个交点即可,则可知,当相切时有一个,则此时的切点的斜率为a,即 ,那么当x>0时,则可值只有实数a的取值范围是
,那么当x>0时,则可值只有实数a的取值范围是 ,但是端点值不能取到,故答案为
,但是端点值不能取到,故答案为 。
。
考点:函数的零点与方程的关系
点评:本题考查了函数的零点与方程的关系,函数的零点就是使得函数y=f(x)的函数值为0时的实数x的值.函数的零点y=f(x)就是方程f(x)=0的实数根,从图象上看,函数的零点y=f(x)就是它的图象与x轴交点的横坐标.因此,函数的零点的研究就可转化为相应函数图象的交点的问题,数形结合的思想得到了很好的体现


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
函数 的定义域为D,若对任意的
的定义域为D,若对任意的 、
、 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在D上为“非减函数”.设函数
在D上为“非减函数”.设函数 在
在 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3)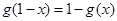 ,则
,则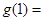 、
、 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若函数 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为M上的t级类增函数。给出4个命题
为M上的t级类增函数。给出4个命题
①函数 上的3级类增函数
上的3级类增函数
②函数 上的1级类增函数
上的1级类增函数
③若函数 上的
上的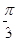 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2
④设 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 是
是 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。
以上命题中为真命题的是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com