
【题目】已知数列![]() 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数![]() 构成等差数列
构成等差数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
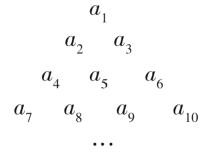
(1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)160;(2)![]() 或
或![]() .
.
【解析】
试题(I)由等差数列{bn}满足b1=a1=1,S5=15.求出数列的公差后,可得数列的通项公式,结合数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,a9=16,可求出公比,进而求出a50的值;
(Ⅱ)由(1)求出Sn的表达式,利用裂项相消法求出Tn的表达式,进而将不等式恒成立问题,转化为最值问题,利用导数法,可得答案.
试题解析:
(1)设等差数列![]() 的公差为
的公差为![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
设从第3行起,每行的公比都是![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,故
,故![]() 是数阵中第10行的第5个数.
是数阵中第10行的第5个数.
故![]() .
.
(2)∵![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
令![]() ,
,
则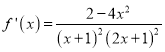
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 为递减数列,
为递减数列,![]() 的最大值为
的最大值为![]() .
.
∴不等式变为![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
则 ,即
,即 ,解得
,解得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
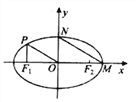
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
(1)求椭圆方程;
(2)过点![]() 且不垂直于坐标轴的直线与椭圆交于
且不垂直于坐标轴的直线与椭圆交于![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知多面体![]() 的直观图(图1)和它的三视图(图2),
的直观图(图1)和它的三视图(图2),


(1)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值,并证明你的结论;若不存在,说明理由;
的值,并证明你的结论;若不存在,说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中![]() 的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中
的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中![]() 都是青年人.
都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,完成![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据判断,能否在犯错误的概率不超过![]() 的前提下认为“经常使用微信与年龄有关”?
的前提下认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com