
分析 (1)先求出函数的对称轴,结合根的判别式求出a,b的值即可;
(2)先求出函数的对称轴,得到函数的单调性,从而求出函数的最大值和最小值;
(3)通过讨论m的范围,得到关于m的方程,从而求出m的值即可.
解答 解:(1)因为二次函数f(x)=ax2+bx+a的对称轴为x=$\frac{7}{4}$,
所以-$\frac{b}{2a}$=$\frac{7}{4}$,
又方程f(x)=7x+a有两个相等的实数根,
所以方程f(x)=7x+a的判别式△=(b-7)2-4a•0=0,
故b=7,a=-2,
∴f(x)=-2x2+7x-2;
(2)由(1)得:f(x)=-2${(x-\frac{7}{4})}^{2}$+$\frac{33}{8}$,对称轴x=$\frac{7}{4}$,
f(x)在[1,3]上的最大值是f($\frac{7}{4}$)=-2×${(\frac{7}{4})}^{2}$+7×$\frac{7}{4}$-2=$\frac{33}{8}$,
f(x)在[1,3]上的最小值是f(3)=-2×32+7×3-2=1,
所以f(x)在[1,3]上的值域是[1,$\frac{33}{8}$];
(3)由(2)知f(3)=1,
若m=$\frac{7}{4}$,则3m≠$\frac{33}{8}$,不符合,
那么m>$\frac{7}{4}$,
则f(m)=-2m2+7m-2=3m,
解得:m=1,不符合,
故不存在实数m满足已知条件.
点评 不同考查了二次函数的性质,考查函数的单调性、最值问题,考查分类讨论,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
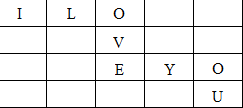 将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)
将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{7}{3}$,+∞) | B. | [$\frac{7}{3}$,4) | C. | ($\frac{7}{3}$,$\frac{11}{3}$] | D. | ($\frac{11}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,0) | B. | (0,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$) | D. | ($\frac{3π}{4}$,π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com