
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
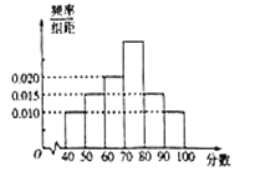
(Ⅰ)求得分在![]() 上的频率;
上的频率;
(Ⅱ)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)以频率估计概率,若在全部参与学习的居民中随机抽取5人参加问卷调查,记得分在![]() 间的人数为
间的人数为![]() ,求
,求![]() 的分布列.
的分布列.
科目:高中数学 来源: 题型:
【题目】已知点N在曲线![]() 上,直线
上,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,动点
,动点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]()
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上 (
上 (![]() 为坐标原点),求证:
为坐标原点),求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上位于第一象限的任一点,且当
是椭圆上位于第一象限的任一点,且当![]() 时,
时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 上点
上点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,过点
对称,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(ⅰ)求![]() 面积最大值;
面积最大值;
(ⅱ)证明:直线![]() 与
与![]() 斜率之积为定值.
斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数数列![]() ,
,![]() 满足:对任意
满足:对任意![]() ,
,![]() ,都有
,都有![]() 恒成立,则称数列
恒成立,则称数列![]() ,
,![]() 为“友好数列”.
为“友好数列”.
(1)已知数列![]() ,
,![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,求证:数列
,求证:数列![]() ,
,![]() 为“友好数列”;
为“友好数列”;
(2)已知数列![]() ,
,![]() 为“友好数列”,且
为“友好数列”,且![]() ,求证:“数列
,求证:“数列![]() 是等差数列” 是“数列
是等差数列” 是“数列![]() 是等比数列”的充分不必要条件.
是等比数列”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.
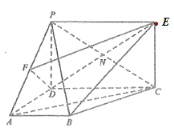
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市调硏机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
月收入(单位:百元) |
|
|
|
|
|
|
频数 | 5 |
| 10 | 5 | 5 | |
频率 | 0.1 |
|
| 0.2 | 0.1 | 0.1 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若所抽调的50名市民中,收入在![]() 的有15名,求
的有15名,求![]() ,
,![]() ,
,![]() 的值,并完成频率分布直方图.
的值,并完成频率分布直方图.
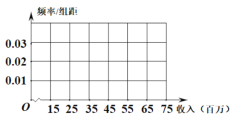
(2)若从收入(单位:百元)在![]() 的被调查者中随机选取2人进行追踪调查,选中的2人中恰有
的被调查者中随机选取2人进行追踪调查,选中的2人中恰有![]() 人赞成“楼市限购令”,求
人赞成“楼市限购令”,求![]() 的分布列与数学期望.
的分布列与数学期望.
(3)从月收入频率分布表的6组市民中分别随机抽取3名市民,恰有一组的3名市民都不赞成“楼市限购令”,根据表格数据,判断这3名市民来自哪组的可能性最大?请直接写出你的判断结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com