
【题目】求函数y=sin(2x﹣ ![]() )的单调递减区间,并叙述怎样由函数y=sinx的图像变换得到函数y=sin(2x﹣
)的单调递减区间,并叙述怎样由函数y=sinx的图像变换得到函数y=sin(2x﹣ ![]() )的图像.
)的图像.
【答案】解:由2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得到:kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,即函数y=sin(2x﹣
,k∈Z,即函数y=sin(2x﹣ ![]() )的单调递减区间为
)的单调递减区间为 ![]() ,k∈Z;
,k∈Z;
将函数y=sinx的图像所有点的横坐标缩短到原来的一半,纵坐标不变得到函数y=sin2x的图像,再将函数y=sin2x的图像向右平移 ![]() 个单位得到函数y=sin(2x﹣
个单位得到函数y=sin(2x﹣ ![]() )的图像
)的图像
【解析】根据正弦函数图像的性质写出函数y=sin(2x﹣ ![]() )的单调递减区间,由函数y=sin x的图像变换得到y=Asin(ωx+φ)(A>0,ω>0)的图像的方法写出由函数y=sinx的图像变换得到函数y=sin(2x﹣
)的单调递减区间,由函数y=sin x的图像变换得到y=Asin(ωx+φ)(A>0,ω>0)的图像的方法写出由函数y=sinx的图像变换得到函数y=sin(2x﹣ ![]() )的图像的变换过程.
)的图像的变换过程.
【考点精析】根据题目的已知条件,利用正弦函数的单调性的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),将f(x)图像沿x轴向右平移 ![]() 个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣
个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣ ![]() )的图像相同,那么y=f(x)的解析式为( )
)的图像相同,那么y=f(x)的解析式为( )
A.f(x)=2sin(2x﹣ ![]() )
)
B.f(x)=2sin(2x﹣ ![]() )
)
C.f(x)=2sin(2x+ ![]() )
)
D.f(x)=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要建造一个长方体无盖贮水池,其容积为6400m3 , 深为4m,如果池底每1m2的造价为300元,池壁每1m2的造价为240元,问怎样设计水池能使总造价最低,最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x∈R,都有ax2>﹣ax﹣1(a≠0)恒成立;命题q:圆x2+y2=a2与圆(x+3)2+(y﹣4)2=4外离.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
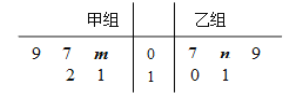
(1)分别求出![]() 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关x的一元二次方程9x2+6ax﹣b2+4=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com