
分析 由已知求出原图的面积,进而根据原图面积与直观图面积的关系,求出直观图的关系,设直观图的高为h,结合直观图中梯形的两底长不变,构造关于h的方程,可得答案.
解答 解:∵四边形OABC是上底为2,下底为6,底角为45°的等腰梯形,
故OABC的高为2,面积S=$\frac{1}{2}$×(2+6)×2=8,
故其直观图的面积S′=8×$\frac{\sqrt{2}}{4}$=2$\sqrt{2}$,
设直观图的高为h,则$\frac{1}{2}$×(2+6)×h=2$\sqrt{2}$,
解得:h=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题考查的知识点是平面图形的直观图,其中正理理解直观图中梯形的两底长不变,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b⇒a+c>b+c | B. | a>b,c>0⇒ac>bc | ||
| C. | a>b⇒a2>b2 | D. | a>b且c>d⇒a+c>b+d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{11}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.
如图,A,B,C,D都在同一个与水平垂直的平面内,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
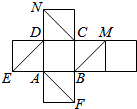 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com