
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
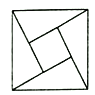
A. 350B. 300C. 250D. 200
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,
两点,![]() 不与
不与![]() 轴垂直,圆
轴垂直,圆![]() .
.
(1)若点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值;
的最大值;
(2)若过线段![]() 的中点
的中点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从盛满2升纯酒精的容器里倒出1升纯酒精,然后填满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒 次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
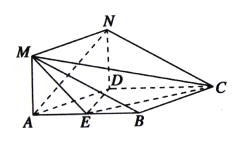
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求![]() 的周长;
的周长;
(2)设点![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在第一象限,点
在第一象限,点![]() 在线段
在线段![]() 上.若
上.若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)设直线![]() 不平行于坐标轴,点
不平行于坐标轴,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .求
.求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,动点
中,动点![]() 与两定点
与两定点![]() 连线的斜率之积为
连线的斜率之积为![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,曲线
两点,曲线![]() 上是否存在点
上是否存在点![]() 使得四边形
使得四边形![]() 为平行四边形?若存在,求直线
为平行四边形?若存在,求直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )

A. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
D. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
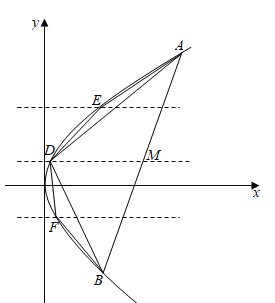
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() 、
、![]() ,且
,且![]() ,
,![]() 是弦
是弦![]() 中点,过
中点,过![]() 作平行于
作平行于![]() 轴的直线交抛物线
轴的直线交抛物线![]() 于点
于点![]() ,得到
,得到![]() ,再分别过弦
,再分别过弦![]() 、
、![]() 的中点作平行于
的中点作平行于![]() 轴的直线依次交抛物线
轴的直线依次交抛物线![]() 于点
于点![]() 、
、![]() ,得到
,得到![]() 和
和![]() ,按此方法继续下去,解决下列问题:
,按此方法继续下去,解决下列问题:
①求证:![]() ;
;
②计算![]() 的面积
的面积![]() ;
;
③根据![]() 的面积
的面积![]() 的计算结果,写出
的计算结果,写出![]() 、
、![]() 的面积,请设计一种求抛物线
的面积,请设计一种求抛物线![]() 与线段
与线段![]() 所围成封闭图形面积的方法,并求此封闭图形的面积.
所围成封闭图形面积的方法,并求此封闭图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com