
【题目】已知下图是四面体![]() 及其三视图,
及其三视图,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
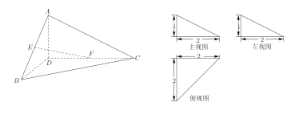
(1)求四面体![]() 的体积;
的体积;
(2)求![]() 与平面
与平面![]() 所成的角;
所成的角;
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由三视图得出四面体的底面![]() 是直角三角形,且可得出两直角边的边长,从而求出底面三角形的面积,由三视图可得出该四面体的高,再利用锥体的体积公式可求出四面体
是直角三角形,且可得出两直角边的边长,从而求出底面三角形的面积,由三视图可得出该四面体的高,再利用锥体的体积公式可求出四面体![]() 的体积;
的体积;
(2)通过![]() 得出点
得出点![]() 到平面
到平面![]() 的距离,利用直线与平面所成角的定义得出直线
的距离,利用直线与平面所成角的定义得出直线![]() 与平面
与平面![]() 所成角的正弦值,从而可求出直线
所成角的正弦值,从而可求出直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(1)由三视图可知,四面体![]() 是直三棱锥,且底面
是直三棱锥,且底面![]() 是以
是以![]() 为直角的直角三角形,
为直角的直角三角形,![]() ,则
,则![]() 的面积为
的面积为![]() ,
,
由三视图可知,![]() 底面
底面![]() ,且
,且![]() ,
,
因此,四面体![]() 的体积为
的体积为![]() ;
;
(2)![]() 是
是![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() ,
,
![]() ,
,
由勾股定理![]() ,
,![]() ,
,
![]() 的
的![]() 边上的高为
边上的高为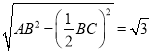 ,
,
![]() ,
,![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,解得
,解得![]() ,
,
连接![]() ,则
,则![]() ,
,![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
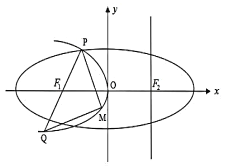
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (
(![]() )的左右两个焦点分别是
)的左右两个焦点分别是![]() 、
、![]() ,
,![]() 在椭圆
在椭圆![]() 上运动.
上运动.
(1)若对![]() 有最大值为120°,求出
有最大值为120°,求出![]() 、
、![]() 的关系式;
的关系式;
(2)若点![]() 是在椭圆上位于第一象限的点,过点
是在椭圆上位于第一象限的点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过
,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,若直线
,若直线![]() 、
、![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)若设![]() ,在(2)成立的条件下,试求出
,在(2)成立的条件下,试求出![]() 、
、![]() 两点间距离的函数
两点间距离的函数![]() ,并求出
,并求出![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为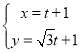 ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
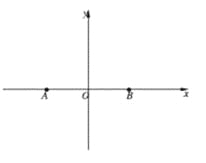
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com