
【题目】已知椭圆![]() 的长轴长为4,右焦点为
的长轴长为4,右焦点为![]() ,且椭圆
,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值与最大值的积为1,圆
的距离的最小值与最大值的积为1,圆![]() 与
与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的取值范围.
的面积乘积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据题意,列出![]() 的方程,根据
的方程,根据![]() ,求出
,求出![]() 的值即可求解;
的值即可求解;
(2)联立直线![]() 和椭圆方程得到关于
和椭圆方程得到关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,利用韦达定理和弦长公式求出
,利用韦达定理和弦长公式求出![]() 的表达式,利用直线
的表达式,利用直线![]() 与
与![]() 相切得到
相切得到![]() 的关系式,由题意知,
的关系式,由题意知,![]() ,利用点到直线的距离公式分别求出点
,利用点到直线的距离公式分别求出点![]() 到直线
到直线![]() 的距离,据此即可得到
的距离,据此即可得到![]() 的表达式,利用基本不等式求最值即可求解.
的表达式,利用基本不等式求最值即可求解.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,则由已知得
,则由已知得![]() ,
,
解得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由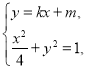 得
得![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]()
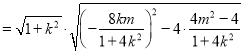
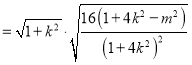 ,
,
因为直线![]() 与
与![]() 相切,所以点
相切,所以点![]() 到直线
到直线![]() 的距离
的距离![]() ,即
,即![]() ,
,
所以![]() ,由
,由![]() ,得
,得![]() ,
,
因为圆![]() 与
与![]() 轴交于
轴交于![]() 两点,所以
两点,所以![]() ,
,
所以![]() 两点到直线
两点到直线![]() 的距离分别为
的距离分别为![]() ,
,
所以![]() 的面积与
的面积与![]() 的面积乘积为
的面积乘积为
![]()

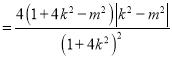
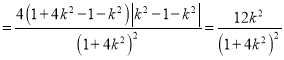
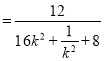 ,
,
因为![]() ,所以
,所以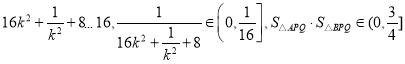 .
.
因此![]() 的面积与
的面积与![]() 的面积乘积的取值范围为
的面积乘积的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动,凡是一次性购物满百元者可以从抽奖箱中一次性任意摸出2个小球(抽奖箱内共有5个小球,每个小球大小形状完全相同,这5个小球上分别标有1,2,3,4,5 这5个数字).
(1)列出摸出的2个小球的所有可能的结果.
(2)已知该超市活动规定:摸出的2个小球都是偶数为一等奖;摸出的2个小球都是奇数为二等奖.请分别求获得一等奖的概率与获得二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季受新冠肺炎疫情的影响,利用网络软件办公与学习成为了一种新的生活方式,网上办公软件的开发与使用成为了一个热门话题.为了解“钉钉”软件的使用情况,“钉钉”公司借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
35岁及以下 | 70 | 30 | 100 |
35岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关?
(2)现从所抽取的35岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用“钉钉”软件的概率.
参考公式: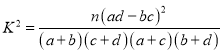 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线一定经过样本点的中心![]()
B.若两个具有线性相关关系的变量的相关性越强,则线性相关系数![]() 的值越接近于1
的值越接近于1
C.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D.在线性回归模型中,相关指数![]() 越接近于1,说明回归模型的拟合效果越好
越接近于1,说明回归模型的拟合效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 为
为![]() 上一动点,过
上一动点,过![]() 作直线
作直线![]() ,
,![]() 为
为![]() 的中垂线,
的中垂线,![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线Γ.
的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若过![]() 的直线与Γ交于
的直线与Γ交于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 与
与![]() 的比值.
的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学跑步骑行交友及健身饮食指导装备购买等--站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程不仅如此,它还可以根据不同人的体质,制定不同的健身计划小吴根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图根据该折线图,下列结论正确的是( ).

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天然气已经进入了千家万户,某市政府为了对天然气的使用进行科学管理,节约气资源,计划确定一个家庭年用量的标准.为此,对全市家庭日常用气的情况进行抽样调查,获得了部分家庭某年的用气量(单位:立方米).将统计结果绘制成下面的频率分布直方图(如图所示).由于操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.若以各组区间中点值代表该组的取值,则估计全市家庭年均用气量约为( )
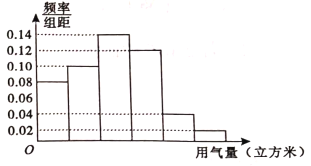
A.6.5立方米B.5立方米C.4.5立方米D.2.5立方米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com