
分析 (1)设圆心(2a,2+a),圆C半径为r,则圆方程为(x-2a)2+(y-2-a)2=r2.再把点A(3,3),B(2,4)代入,求得a、r的值,可得圆C方程.
(2)由条件直线y=kx+2与圆C有两个不同的交点,可得$\frac{|2k-3+2|}{\sqrt{{k}^{2}+1}}$<1,由此求得k的取值范围.
解答 解:(1)设圆心(2a,2+a),圆C半径为r,∴圆方程为(x-2a)2+(y-2-a)2=r2.
再把点A(3,3),B(2,4)代入可得(3-2a)2+(3-2-a)2=(2-2a)2+(4-2-a)2=r2,
∴a=1,r=1,
∴圆C方程为(x-2)2+(y-3)2=1.
(2)∵直线y=kx+2与圆C有两个不同的交点,
∴$\frac{|2k-3+2|}{\sqrt{{k}^{2}+1}}$<1,∴0<k<$\frac{4}{3}$.
点评 本题主要考查求圆的标准方程的方法,本题主要考查直线和圆相交的性质,点到直线的距离公式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为π的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
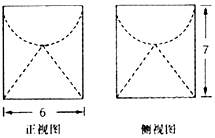 某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )
某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )| A. | 60π | B. | 75π | C. | 90π | D. | 93π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
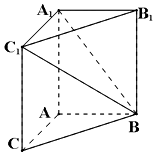 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com