Question

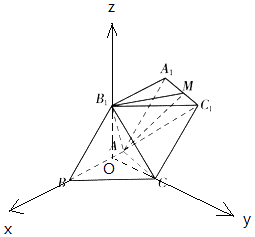
【题目】如图，已知斜三棱柱ABC﹣A1B1C1的所有棱长均为2，∠B1BA= ，且侧面ABB1A1⊥底面ABC． （Ⅰ）证明：B1C⊥AC1
（Ⅱ）若M为A1C1的中点，求二面角A﹣B1M﹣A1的余弦值．

Answer 1

【答案】（Ⅰ）证明：过B1作BO⊥平面ABC， ∵斜三棱柱ABC﹣A1B1C1的所有棱长均为2，∠B1BA= ，
M，N分别为A1C1与B1C的中点，且侧面ABB1A1⊥底面ABC．
∴△ABC和△ABB1是边长为2的等边三角形，∴O是AB中点，∴B1O= ，
∴OB，OB1 ， OC两两垂直，
以O为原点，OB为x轴，OC为y轴，OB1为z轴，建立空间直角坐标系，
则O（0，0，0），B1（0，0， ），C（0， ，0），A（﹣1，0，0），C1（﹣1， ， ），
=（0， ）， =（0， ），
∴ =0+3﹣3=0，
∴B1C⊥AC1 ．
（Ⅱ）解：∵M为A1C1的中点，A1（﹣2，0， ），A（﹣1，0，0），B1（0，0， ），C1（﹣1， ， ），M（﹣ ， ， ），
∴ =（1，0， ）， =（﹣ ， ， ），
设平面AB1M的法向量 =（x，y，z），
则 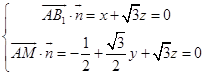，取z=1，得 =（﹣ ，3，1），
平面B1MA1的法向量 =（0，0，1），
设二面角A﹣B1M﹣A1的平面角为θ，
则cosθ= = = ．
∴二面角A﹣B1M﹣A1的余弦值为 ．

【解析】（Ⅰ）过B1作BO⊥平面ABC，则OB，OB1 ， OC两两垂直，以O为原点，OB为x轴，OC为y轴，OB1为z轴，建立空间直角坐标系，利用向量法能证明B1C⊥AC1 ． （Ⅱ）求出平面AB1M的法向量和平面B1MA1的法向量，利用向量法能求出二面角A﹣B1M﹣A1的余弦值．
【考点精析】关于本题考查的直线与平面垂直的性质，需要了解垂直于同一个平面的两条直线平行才能得出正确答案．