考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求导,根据导数与0的关系,求出函数的单调区间;
(Ⅱ)构造函数g(x)=f(x)-(6x
2+6x),利用导数求出函数g(x)
max=0,问题得以证明.
(Ⅲ)构造函数h(x)=f(
)-
,求出导数,再利用放缩法得到h′(x)≤
-
,再构造函数p(x)=(x+5)(x+3)
2-96x,
利用导数求出函数的最大值为0,继而求出函数h(x)为减函数,问题得以证明
解答:
解:(Ⅰ)∵f(x)=2x+2ln(2x+1)
∴函数的定义域(-
,+∞),
∴f′(x)=2+
>0恒成立,
故函数在(-
,+∞)为增函数;
(Ⅱ)令g(x)=f(x)-(6x
2+6x)
∴g′(x)=f′(x)-(12x+6)=-4•
令g′(x)=0,解得x=0,
当g′(x)>0,解得
-<x<0,函数g(x)单调递增,
当g′(x)<0,解得x>0,函数g(x)单调递减,
∴当x=0时,函数有最大值,即g(x)≤g(0)=0,
∴f(x)≤6x
2+6x;
(Ⅲ)f(
)=2×
+2ln(2×
+1)=
-1+2ln
=
-1+lnx
令h(x)=f(
)-
=lnx+
-1-
,
∴h′(x)=
+
-
∵x∈(1,3),
∴
+
=
=
=
≤
∴h′(x)≤
-
=
,
再令p(x)=(x+5)(x+3)
2-96x=x
3+11x
2-57x+45,
∴p′(x)=3x
2+22x-57,
∵p′(1)=-32<0,p′(3)=36>0,
∴存在x
0∈(1,3)时,使得p′(x
0)=0,
∴x∈(1,x
0),p′(x
0)<0,
x∈(x
0,3),p′(x
0)>0,
∴函数p(x)在(1,x
0)递减,在(x
0,3)上递增,
∵p(1)=96-96=0,P(3)=288-299=0,
∴x∈(1,3)时,恒有p(x)≤p(x)
max=0,
∴h′(x)<0,在(1,3)上恒成立,
∴函数h(x)在(1,3)上递减,
∴x∈(1,3)时.h(x)<h(1)=0,
即(x+3)f(
)<6x-6.
点评:本题考查了导数和函数的单调性最值的关系,以及利用导数来证明不等式成立的问题,需要多次构造函数,多次求导,培养了学生的转化能力,运算能力,属于难题



 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案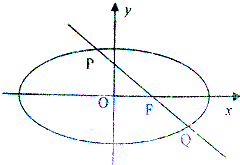 已知椭圆的中心在原点,右焦点为F(3,0)过焦点F的直线l交P,Q两点线段PQ的中点为M(2,1).求:
已知椭圆的中心在原点,右焦点为F(3,0)过焦点F的直线l交P,Q两点线段PQ的中点为M(2,1).求: