
【题目】【2017唐山模拟】如图,ABCDA1B1C1D1为正方体,连接BD,AC1,B1D1, CD1,B1C,现有以下几个结论:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是;④CB1与BD为异面直线,其中所有正确结论的序号为________.

科目:高中数学 来源: 题型:
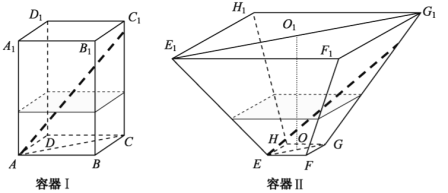
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ≤a≤1,若函数f(x)=ax2﹣2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)﹣N(a).
≤a≤1,若函数f(x)=ax2﹣2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)﹣N(a).
(1)求g(a)的函数表达式;
(2)判断函数g(a)在区间[ ![]() ,1]上的单调性,并求出g(a)的最小值.
,1]上的单调性,并求出g(a)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
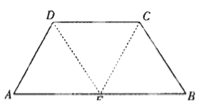
【题目】【2017开封高三模拟理】如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
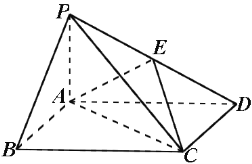
【题目】【2014高考课标2理数18】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦的长度为1.
相交所得弦的长度为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,设
,设![]() ,
, ![]() ,其中
,其中![]() 为坐标原点.当以线段
为坐标原点.当以线段![]() 为直径的圆恰好过点
为直径的圆恰好过点![]() 时,求证:
时,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体素质情况,现从我校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示.根据有关国家标准,成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)从前文所指的这10人(成绩见茎叶图)中随机选取3人,记![]() 表示测试成绩为“优秀”的学生人数,求
表示测试成绩为“优秀”的学生人数,求![]() 的分布列及期望.
的分布列及期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com