
【题目】设函数![]() .
.
(1)若不等式![]() 的解集是
的解集是![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)当![]() 时,对任意的
时,对任意的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了
公司从某大学招收毕业生,经过综合测试,录用了![]() 名男生和
名男生和![]() 名女生,这
名女生,这![]() 名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在
名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在![]() 分以上者到甲部门工作;
分以上者到甲部门工作;![]() 分以下者到乙部门工作,另外只有成绩高于
分以下者到乙部门工作,另外只有成绩高于![]() 分才能担任助理工作。
分才能担任助理工作。
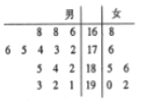
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,那么至少有一人是甲部门人选的概率是多少?
人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选![]() 人,用
人,用![]() 表示所选人员中能担任助理工作的男生人数,写出
表示所选人员中能担任助理工作的男生人数,写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
性别与读营养说明列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(Ⅰ)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(Ⅱ)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:![]() ,其中
,其中![]() 为样本容量.)
为样本容量.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.(1)设该辆轿车使用
万元.(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面是正三角形)中,
(侧棱垂直于底面,且底面是正三角形)中,![]() 是棱
是棱![]() 上一点.
上一点.
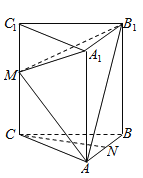
(1)若![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:不论![]() 在何位置,四棱锥
在何位置,四棱锥![]() 的体积都为定值,并求出该定值.
的体积都为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面是正三角形)中,
(侧棱垂直于底面,且底面是正三角形)中,![]() 是棱
是棱![]() 上一点.
上一点.
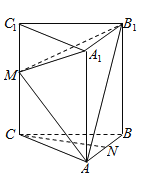
(1)若![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 上靠近点
上靠近点![]() 的一个三等分点,求二面角
的一个三等分点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() 是6与
是6与![]() 的等差中项
的等差中项![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使不等式
,使不等式![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com