
【题目】曲线![]() ,直线
,直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】给出下列两组数据:甲:12,13,11,10,14.乙:10,17,10,13,10.
(1)分别计算两组数据的平均差,并根据计算结果判断哪组数据波动大.
(2)分别计算两组数据的方差,并根据计算结果判断哪组数据波动大.
(3)以上两种判断方法的结果是否一致?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7,8,6,9,6,5,9,9,7,4.
乙:9,5,7,8,7,6,8,6,7,7.
(1)分别计算甲、乙两人射击命中环数的极差、众数和中位数;
(2)分别计算甲、乙两人射击命中环数的平均数、方差、标准差;
(3)比较两人的成绩,然后决定选择哪一个人参赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若AC⊥BC,AC=BC=1,点P是△ABC内一点,则![]() 的取值范围是( )
的取值范围是( )
A. (﹣![]() ,0) B. (0,
,0) B. (0,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为![]() 的函数
的函数![]() 同时满足以下三条:
同时满足以下三条:
(ⅰ)对任意的![]() 总有
总有![]() (ⅱ)
(ⅱ)![]()
(ⅲ)若![]() 则有
则有![]() 就称
就称![]() 为“A函数”,下列定义在
为“A函数”,下列定义在![]() 的函数中为“A函数”的有_______________
的函数中为“A函数”的有_______________
①![]() ;②
;②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数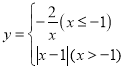 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
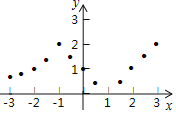
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
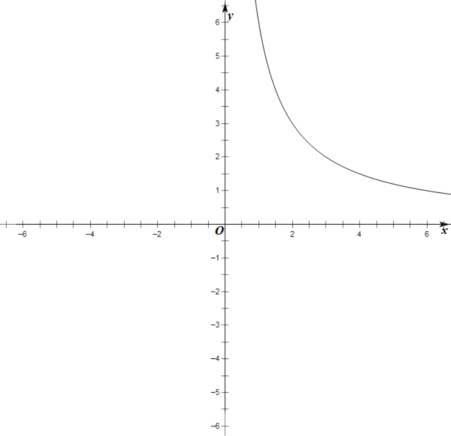
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com