
分析 (1)利用导数求函数的单调区间,从而求解函数f(x)的极值;
(2)设切线l2的方程为y=k2x,从而由导数及斜率公式可求得切点为(1,e),k2=e;再设l1的方程,整理得$ln{x_1}-1+\frac{1}{x_1}-\frac{1}{e}=0$,再令$m(x)=lnx-1+\frac{1}{x}-\frac{1}{e}$,求导确定函数的单调性,从而问题得证.
解答 (1)解:$f'(x)=\frac{1}{x}-a$
①若a≤0时,$f'(x)=\frac{1}{x}-a$>0
所以函数f(x)在(0,+∞)单调递增,故无极大值和极小值
②若a>0,由$f'(x)=\frac{1}{x}-a=0$得$x=\frac{1}{a}$,
所以$x∈(0,\frac{1}{a})$.函数f(x)单调递增,$x∈(\frac{1}{a},+∞)$,函数f(x)单调递减
故函数f(x)有极大值a-lna-1,无极小值.
(2)证明:设切线l2的方程为y=k2x,切点为(x2,y2),
则${y_2}={e^{x_2}}$,${k_2}={e^{x_2}}=\frac{y_2}{x_2}$,所以x2=1,y2=e,则${k_2}={e^{x_2}}=e$.
由题意知,切线l1的斜率为${k_1}=\frac{1}{k_2}=\frac{1}{e}$,l1的方程为$y={k_1}x=\frac{1}{e}x$.
设l1与曲线y=f(x)的切点为(x1,y1),则${k_1}=f'({x_1})=\frac{1}{x_1}-a$=$\frac{1}{e}=\frac{y_1}{x_1}$,
所以${y_1}=\frac{x_1}{e}=1-a{x_1}$,$a=\frac{1}{x_1}-\frac{1}{e}$.
又因为y1=lnx1-a(x1-1),消去y1和a后,整理得$ln{x_1}-1+\frac{1}{x_1}-\frac{1}{e}=0$
令$m(x)=lnx-1+\frac{1}{x}-\frac{1}{e}$,则$m'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,
所以m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
又x0为m(x)的一个零点,所以
①若x1∈(0,1),因为$m(\frac{1}{e})=-2+e-\frac{1}{e}>0$,$m(1)=-\frac{1}{e}<0$,所以${x_1}∈(\frac{1}{e},1)$,
因为$ln{x_1}-1+\frac{1}{x_1}-\frac{1}{e}=0$
所以$a=\frac{1}{x_1}-\frac{1}{e}$=1-lnx1,所以1<a<2.
②若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x1=e,
所以a=1-lnx1=0(舍去).
综上可知,1<a<2.
点评 本题考查利用导数讨论含参数函数的单调性、利用导数求曲线的切线问题,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明;属于难题.


科目:高中数学 来源: 题型:解答题
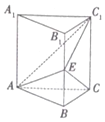 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
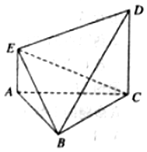 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{6},\frac{5π}{12}}]$ | B. | $[{\frac{5π}{12},π}]$ | C. | $[{\frac{π}{4},π}]$ | D. | $[{\frac{π}{4},\frac{2π}{3}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com