
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,证明:函数
时,证明:函数![]() 只有一个零点;
只有一个零点;
(3)若函数![]() 的极大值等于
的极大值等于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)求得函数在![]() 处的导数,由此求得切线方程.
处的导数,由此求得切线方程.
(2)通过求![]() 的二阶导数,研究其一阶导数,进而求得函数
的二阶导数,研究其一阶导数,进而求得函数![]() 的单调区间,由此证得函数
的单调区间,由此证得函数![]() 只有一个零点.
只有一个零点.
(3)当![]() 时根据(2)的结论证得结论成立.当
时根据(2)的结论证得结论成立.当![]() ,根据
,根据![]() 的二阶导数,对
的二阶导数,对![]() 分成
分成![]() 三种情况,利用
三种情况,利用![]() 的一阶导数,结合零点的存在性定理,求得实数
的一阶导数,结合零点的存在性定理,求得实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() ,令
,令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]() ,所以
,所以![]() 只有一个零点
只有一个零点![]() .
.
(3)①当![]() 时,由(2)知,
时,由(2)知,![]() 的极大值为
的极大值为![]() ,符合题意;
,符合题意;
②当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,注意到
单调递减,注意到![]() ,
,
(ⅰ)当![]() 时,
时,![]() ,又
,又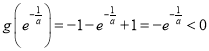 .
.
所以存在![]() ,使得
,使得![]() ,当
,当![]() 时,
时, ![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() 的极大值为
的极大值为![]() ,符合题意;
,符合题意;
(ⅱ)当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减,无极值,不合题意;
上单调递减,无极值,不合题意;
(ⅲ)当![]() 时,
时,![]() ,又
,又![]() ,令
,令![]()
![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ,
,
存在![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() 的极大值为
的极大值为![]() ,且
,且![]() ,不合题意.
,不合题意.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() 。
。
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)若![]() ,问函数
,问函数![]() 有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样.
②某地气象局预报:5月9日本地降水概率为![]() ,结果这天没下雨,这表明天气预报并不科学.
,结果这天没下雨,这表明天气预报并不科学.
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:集合
满足:集合![]() 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数![]() 是等比源函数.
是等比源函数.
(![]() )判断下列函数:①
)判断下列函数:①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(![]() )判断函数
)判断函数![]() 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
(![]() )证明:
)证明: ![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数![]() ,椭圆
,椭圆![]() 的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线
的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线![]() 于点M.
于点M.
![]() 若点P的横坐标为1,求点Q的横坐标;
若点P的横坐标为1,求点Q的横坐标;
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 为坐标原点,离心率为
为坐标原点,离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
(2)![]() 为椭圆上三个动点,
为椭圆上三个动点,![]() 在第二象限,
在第二象限,![]() 关于原点对称,且
关于原点对称,且![]() ,判断
,判断![]() 是否存在最小值,若存在,求出该最小值,并求出此时点
是否存在最小值,若存在,求出该最小值,并求出此时点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com