Question

已知圆x²+y²=1，点A(1，0)，△ABC内接于该圆，且∠BAC=60°，当B、C在圆上运动时，求BC的中点的轨迹方程.

Answer 1

解析:本题是比较典型的使用曲线的参数方程来解决相关问题的题目，涉及到多个点的坐标，怎样比较巧妙地把相关点的坐标给表示出来，从而找到所要求的问题的解.显然借助于圆的参数方程就容易将点B、C的坐标给表示出来，进而把其中的点的坐标给表示出来；然后通过消去参数从而达到目的，之后还要注意其中的参数的取值范围.

解:如图(1)所示，M为BC的中点，?

由∠BAC=60°，得∠BOC=2×60°=120°,(弦所对的圆心角等于它所对的圆周角的2倍)?

在△BOC中，OB=OC=1OM=.所以点M的轨迹方程为x²+y²=.?

   

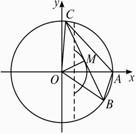
(1)　　            (2)

又因为x≥时，如图(2),

虽然∠BOC=120°，

但∠BAC=(360°-120°)=120°≠60°,

所以点M的轨迹方程为x²+y²=(x＜),如图(2).

点评:本题主要容易忽视隐含的范围x＜，忽视了这个范围则本题的解答就不严谨，并且很多资料上的答案也都没有这个范围，像这样的求轨迹的问题一定要注意这一点.