
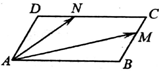
 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
分析 画出图形,建立直角坐标系,利用比例关系,求出M,N的坐标,然后通过二次函数求出数量积的范围.
解答 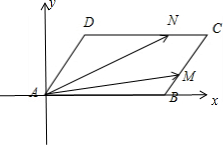 解:建立如图所示的直角坐标系,则B(2,0),A(0,0),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
解:建立如图所示的直角坐标系,则B(2,0),A(0,0),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
∵$\frac{BM}{BC}=\frac{NC}{DC}=λ$,λ∈[0,1],
$\overrightarrow{AM}$=$\overrightarrow{AB}$+λ$\overrightarrow{BC}$=$\overrightarrow{AB}$+λ$\overrightarrow{AD}$=M(2+$\frac{λ}{2}$,$\frac{\sqrt{3}}{2}$λ),
即M(2+$\frac{λ}{2}$,$\frac{\sqrt{3}}{2}$λ);
$\overrightarrow{AN}$=$\overrightarrow{AD}+\overrightarrow{DN}$=$\overrightarrow{AD}$+($\overrightarrow{DC}$-λ$\overrightarrow{DC}$)=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)+(1-λ)•(2,0)=($\frac{5}{2}$-2λ,$\frac{\sqrt{3}}{2}$),
即 N($\frac{5}{2}$-2λ,$\frac{\sqrt{3}}{2}$).
所以$\overrightarrow{AM}$=(2+$\frac{λ}{2}$,$\frac{\sqrt{3}}{2}$λ)•($\frac{5}{2}$-2λ,$\frac{\sqrt{3}}{2}$)=-λ2-2λ+5=-(λ+1)2+6.
因为λ∈[0,1],二次函数的对称轴为:λ=-1,
故当λ∈[0,1]时,-λ2-2λ+5∈[2,5].
故选:C.
点评 本题考查向量的综合应用,平面向量的坐标表示以及数量积的应用,二次函数的最值问题,考查计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
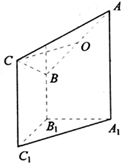 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
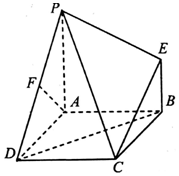 如图,四边形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F为PD的中点.
如图,四边形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13和-11 | B. | 8和-6 | C. | 1和-3 | D. | 3和-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com