
����Ŀ�����й��ڸ��ʺ�ͳ�Ƶļ���˵����
��10������ij������ͬһ������������ļ����ֱ���15��17��14��10��15��17��17��16��14��12������ƽ����Ϊa����λ��Ϊb������Ϊc����a��b��c�Ĵ�С��ϵΪc��a��b��
������4��2��1��0����2�ı�����2��
�������ΪS�ġ�ABC����ѡһ��P��������¼�����PBC�����С��![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() ��
��
�ܴ�д��0��1��2������9��ʮ�ſ�Ƭ�У��зŻص�ÿ�γ�һ�ţ��������Σ������ſ�Ƭ�ϵ����ָ�����ͬ�ĸ�����![]() .
.
������ȷ˵���������________��
���𰸡��ڢ�
��������
�ٸ���ƽ��������λ���������Ķ�����бȽϼ������ڸ��ݱ���Ĺ�ʽ�����ж����۸��ݼ��θ��͵ĸ��ʹ�ʽ��������ж����ܸ��ݹŵ�����ʸ��ʹ�ʽ�����жϣ�
���ڢ٣�������ԭ����Ϊ10��12��14��14��15��15��16��17��17��17���ʿɵø������ݵ�ƽ����![]() ����λ��
����λ��![]() ������Ϊ
������Ϊ![]() ������
������![]() ���ʢٲ���ȷ��
���ʢٲ���ȷ��
���ڢڣ��������������ƽ����Ϊ1��
�ʷ���Ϊ![]() �����Ա���Ϊ2���ʢ���ȷ��
�����Ա���Ϊ2���ʢ���ȷ��
���ڢ�����ͼ��������ABC�ĸ�![]() ������PBC���������
������PBC���������![]() ʱ��
ʱ��![]() ��
��
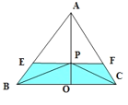
Ҫʹ��PBC�����С��![]() �����PӦλ��ͼ�е���Ӱ�����ڣ�
�����PӦλ��ͼ�е���Ӱ�����ڣ�
������ɵ�![]() ����
����![]() ��
��
�����ɼ��θ����ʹ�ʽ�ɵ�����PBC�����С��![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() ���ʢ۲���ȷ��
���ʢ۲���ȷ��
���ڢܣ�����������еĻ����¼�����Ϊ![]() �����¼����зŻص�ÿ�γ�һ�ţ��������Σ������ſ�Ƭ�ϵ����ָ�����ͬ�������Ļ����¼���
�����¼����зŻص�ÿ�γ�һ�ţ��������Σ������ſ�Ƭ�ϵ����ָ�����ͬ�������Ļ����¼���![]() �������ݹŵ���͵ĸ��ʹ�ʽ���������Ϊ
�������ݹŵ���͵ĸ��ʹ�ʽ���������Ϊ![]() ��������ȷ��
��������ȷ��
���Ͽɵâڢ���ȷ��
�ʴ�Ϊ�ڢܣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
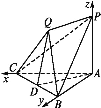
����Ŀ����ͼ,������P-ABC��,PA������ABC,��ABC��ֱ��������,��PA=AB=AC.��ƽ��QBC��ֱ�ڵ���ABC.
(1)��֤:PA��ƽ��QBC;
(2)��PQ��ƽ��QBC,��������Q-PB-A������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x�� ![]() ��e��x��x��
��e��x��x�� ![]() ����
����
������f��x���ĵ�������
������f��x��������[ ![]() ��+�ޣ��ϵ�ȡֵ��Χ��
��+�ޣ��ϵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2px����P��1��1�������㣨0�� ![]() ����ֱ��l��������C���ڲ�ͬ������M��N������M��x��Ĵ��߷ֱ���ֱ��OP��ON���ڵ�A��B������OΪԭ�㣮��14�֣�
����ֱ��l��������C���ڲ�ͬ������M��N������M��x��Ĵ��߷ֱ���ֱ��OP��ON���ڵ�A��B������OΪԭ�㣮��14�֣�
��1����������C�ķ��̣������佹��������߷��̣�
��2����֤��AΪ�߶�BM���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������P-ABCD��,PA������ABCD,����ABCDΪֱ������,AD��BC,��BAD=90��,PA=AD=AB=2BC=2,��AD��ƽ��ֱ�PB,PC��M,N����.

(1)��֤:MN��BC;
(2)��M,N�ֱ�ΪPB,PC���е�,
����֤:PB��DN;
��������P-DN-A������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �İ뾶Ϊ1�� Բ����
�İ뾶Ϊ1�� Բ����![]() ��.
��.

��1����Բ��![]() Ҳ��ֱ��
Ҳ��ֱ��![]() �ϣ�����
�ϣ�����![]() ��Բ
��Բ![]() �����ߣ������߷��̣�
�����ߣ������߷��̣�
��2����Բ![]() �ϴ��ڵ�
�ϴ��ڵ�![]() ��ʹ
��ʹ![]() ����Բ��
����Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij�����������ͼ��ֱ��ͼ��ͼ��ʾ,������ͼΪ����,����ͼΪ����ֱ��������,����ͼΪֱ������.
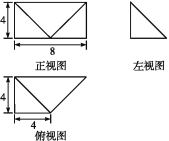
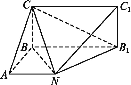
(1)֤��:ƽ��BCN��ƽ��C1NB1;
(2)������C-NB1-C1������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��ֳ������ijˮ��Ʒ���¡���������ֳ�����IJ����Աȣ��ջ�ʱ�������ȡ��100�����䣬��������ˮ��Ʒ�IJ�������λ��kg������Ƶ�ʷֲ�ֱ��ͼ���£� 
����A��ʾʱ�䡰����ֳ�������������50kg��������A�ĸ��ʣ�
������д�������������������������ж��Ƿ���99%�İ�����Ϊ���������ֳ�����йأ�
�������50kg | �������50kg | |
����ֳ�� | ||
����ֳ�� |
�������������Ƶ�ʷֲ�ֱ��ͼ����������ֳ���������ӽ��бȽϣ�
����
P��K2��K�� | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣�����Աÿ��Ӹ��������������ȡ16���������������ߴ磨��λ��cm�������ݳ����������飬������Ϊ��������������״̬������������ijߴ������̬�ֲ�N���̣���2������12�֣�
��1����������״̬��������X��ʾһ���ڳ�ȡ��16���������ߴ��ڣ��̩�3�ң���+3�ң�֮������������P��X��1����X����ѧ������
��2��һ���ڳ������У���������˳ߴ��ڣ��̩�3�ң���+3�ң�֮������������Ϊ��������������һ����������̿��ܳ������쳣�������Ե�����������̽��м�飮
��������˵����������������̷����ĺ����ԣ�
�����������Ǽ���Ա��һ���ڳ�ȡ��16������ijߴ磺
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
������� ![]() =
= ![]() =9.97��s=
=9.97��s= ![]() =
= ![]() ��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
������ƽ���� ![]() ��Ϊ�̵Ĺ���ֵ
��Ϊ�̵Ĺ���ֵ ![]() ������������s��Ϊ�ҵĹ���ֵ
������������s��Ϊ�ҵĹ���ֵ ![]() �����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿����
�����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿���� ![]() ��3
��3 ![]() +3
+3 ![]() ��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
�������������Z������̬�ֲ�N���̣���2������P���̩�3�ң�Z����+3�ң�=0.9974��0.997416��0.9592�� ![]() ��0.09��
��0.09��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com