
【题目】如图所示,平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 为矩形,四边形
为矩形,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)结合已知条件本题可采用向量法求解,证明线面平行只需证明直线的方向向量垂直于平面的法向量;(Ⅱ)中由线面所成角需找到直线的方向向量![]() 与平面的法向量
与平面的法向量![]() ,利用公式
,利用公式![]() 求线面角
求线面角
试题解析:(Ⅰ)(法一)取![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() ,
,
![]() 且
且![]() ,
,
![]() ,则
,则![]() 且
且![]() .
.
![]() 四边形
四边形![]() 为矩形,
为矩形, ![]() 且
且![]() ,
,
![]() 且
且![]() ,
,
![]() ,则
,则![]() .
.
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
法二![]() 四边形
四边形![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,
为矩形,
![]() ,
, ![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]()
![]()
以![]() 为原点,
为原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴建立如图所示空间直角坐标系.
轴建立如图所示空间直角坐标系.
根据题意我们可得以下点的坐标:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
又![]() ,
,
∴![]()
∵![]() 平面
平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的一个法向量为
的一个法向量为![]() ,
, ![]() ,
, ![]() ,则
,则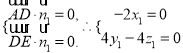 , 取
, 取![]() ,得
,得![]() .
.
![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
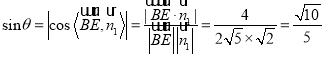 .
.
所以![]()
所以![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
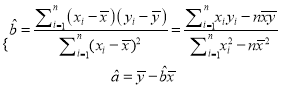
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 、
、![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数![]() ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数![]() ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数![]() ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
A.①② B.③④
C.③④⑤ D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
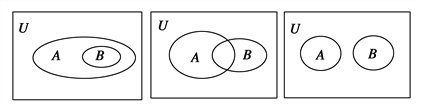
【题目】我们知道,如果集合AS,那么S的子集A的补集为SA={x|x∈S,且xA}.类似地,对于集合A、B,我们把集合{x|x∈A,且xB}叫作集合A与B的差集,记作A-B.据此回答下列问题:
(1)若A={1,2,3,4},B={3,4,5,6},求A-B;
(2)在下列各图中用阴影表示集合A-B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com