
【题目】在极坐标系中,已知曲线C1:ρ=2cosθ,将曲线C1上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C,又已知直线l: 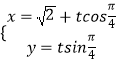 (t是参数),且直线l与曲线C交于A,B两点.
(t是参数),且直线l与曲线C交于A,B两点.
(1)求曲线C的直角坐标方程,并说明它是什么曲线;
(2)设定点P( ![]() ,0),求|PA|+|PB|.
,0),求|PA|+|PB|.
【答案】
(1)解:曲线C1的直角坐标方程为:x2+y2﹣2x=0即(x﹣1)2+y2=1.
∴曲线C的方程为 ![]()
∴曲线C表示焦点坐标为(- ![]() ,0),(
,0),( ![]() ,0),长轴长为4的椭圆
,0),长轴长为4的椭圆
(2)解:将直线l的参数方程代入曲线C的方程: ![]() 中,得
中,得 ![]() .
.
设A、B两点对应的参数分别为t1,t2
则t1+t2=﹣ ![]() ,t1t2=﹣
,t1t2=﹣ ![]() ,
,
∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|= ![]()
【解析】(1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2 , 化曲线C1的方程为(x﹣1)2+y2=1,再由图象变化吧的规律可得曲线C;(2)将直线l的参数方程代入曲线C的方程: ![]() 中,得
中,得 ![]() ,运用韦达定理,参数的几何意义,即可求|PA|+|PB|.
,运用韦达定理,参数的几何意义,即可求|PA|+|PB|.


科目:高中数学 来源: 题型:
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】双曲线的方程为![]() ,则渐近线方程为
,则渐近线方程为![]() ,渐近线方程为:
,渐近线方程为: ![]() ,反之当渐近线方程为
,反之当渐近线方程为![]() 时,只需要满足
时,只需要满足![]() ,等轴双曲线即可.故选择充分不必要条件.
,等轴双曲线即可.故选择充分不必要条件.
故答案为:A.
【题型】单选题
【结束】
10
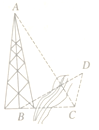
【题目】如图,为测量河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,在点
的正东方向上,在点![]() 处测得
处测得![]() 点的仰角为
点的仰角为![]() ,再由点
,再由点![]() 沿北偏东
沿北偏东![]() 方向走
方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是( )
的高是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,分别过点
两点,分别过点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 和
和![]() ,记
,记![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)证明:直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
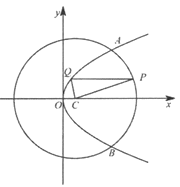
【题目】如图,抛物线W:y2=4x与圆C:(x-1)2+y2=25交于A,B两点,点P为劣弧![]() 上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
A. (10,14) B. (12,14)
C. (10,12) D. (9,11)
查看答案和解析>>
科目:高中数学 来源: 题型:
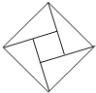
【题目】在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() ,则
,则![]() 的值等于( )
的值等于( )
A. 1 B. ![]() C.
C. ![]()
![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则下列命题:
,则下列命题:
①对任意![]() ,都有
,都有![]() ;②函数
;②函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
③函数![]() 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当![]() 时,
时,![]() .
.
其中正确命题的序号有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() 的焦点为F,直线
的焦点为F,直线![]() 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求C的方程;
(2)过F的直线![]() 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线![]() 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com