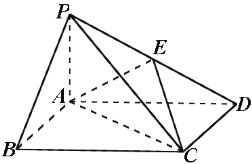
[题目][2014高考课标2理数18]如图.四棱锥P-ABCD中.底面ABCD为矩形.PA⊥平面ABCD.E为PD的中点.(Ⅰ)证明:PB∥平面AEC,(Ⅱ)设二面角D-AE-C为60°.AP=1.AD=.求三棱锥E-ACD的体积. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】【2014高考课标2理数18】如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，

E为PD的中点.

（Ⅰ）证明：PB∥平面AEC；

（Ⅱ）设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积.

【答案】

【解析】（Ⅰ）证明：设O为AC与BD交点，连结OE，则由矩形ABCD知：O为BD的中点，因为E是BD的中点，所以OE∥PB，因为OE面AEC，PB面AEC，所以PB∥平面AEC。

（Ⅱ）以A为原点，直线AB、AD、AP分别为x、y、z轴建立空间直角坐标系，设AB=m，则

是平面AED的一个法向量，设是平面AEC的法向量，则

，解得，，所以令，得，所以

=，因为二面角的大小与其两个半平面的两个法向量的夹角相等哉互补，所以=，解得，因为E是PD的中点，所以三棱锥E-ACD的高为，所以三棱锥E-ACD的体积为==.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．

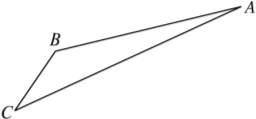
现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min，在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C．假设缆车匀速直线运行的速度为130 m/min，山路AC长为1 260 m，经测量，cos A＝，cos C＝．

（1）求索道AB的长；

（2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？

（3）为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，过椭圆右焦点的直线交椭圆于两点，为的中点，且直线的斜率为．

（Ⅰ）求椭圆的方程；

（Ⅱ）设另一直线与椭圆交于两点，原点到直线的距离为，求面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知多面体如图所示.其中为矩形，为等腰直角三角形，，四边形为梯形，且，， .

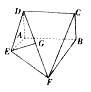
（1）若为线段的中点，求证：平面.

（2）线段上是否存在一点，使得直线与平面所成角的余弦值等于？若存在，请指出点的位置；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

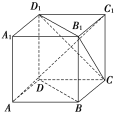
【题目】【2017唐山模拟】如图，ABCDA1B1C1D1为正方体，连接BD，AC1，B1D1， CD1，B1C，现有以下几个结论：①BD∥平面CB1D1；②AC1⊥平面CB1D1；③AC1与底面ABCD所成角的正切值是；④CB1与BD为异面直线，其中所有正确结论的序号为________．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在四棱锥中，平面，，，，，为的中点，为棱上一点．

（Ⅰ）当为何值时，有平面；

（Ⅱ）在（Ⅰ）的条件下，求点到平面的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数f（x）=kax﹣a﹣x（a＞0且a≠1）在（﹣∞，+∞）上既是奇函数又是增函数，则函数g（x）=loga（x+k）的图像是（）
A.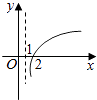
B.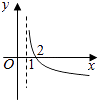
C.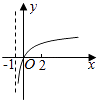
D.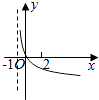

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义在区间（0，+∞）上的函数f（x）=|t（x+ ）﹣5|，其中常数t＞0．
（1）若函数f（x）分别在区间（0，2），（2，+∞）上单调，试求实数t的取值范围；
（2）当t=1时，方程f（x）=m有四个不相等的实根x1 ， x2 ， x3 ， x4 ． ①求四根之积x1x2x3x4的值；
②在[1，4]上是否存在实数a，b（a＜b），使得f（x）在[a，b]上单调且取值范围为[ma，mb]？若存在，求出m的取值范围；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，且.

（1）求函数的极值；

（2）当时，证明：.

查看答案和解析>>

同步练习册答案