
 房屋的天花板上点P处有一光源,P在地面上的射影为Q,在地面上放置正棱锥S-ABCD,底面ABCD接触地面,已知正四棱锥S-ABCD的高为1米,底面ABCD的边长为
房屋的天花板上点P处有一光源,P在地面上的射影为Q,在地面上放置正棱锥S-ABCD,底面ABCD接触地面,已知正四棱锥S-ABCD的高为1米,底面ABCD的边长为| 1 | 2 |
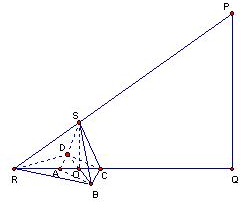 解:欲使得棱锥影子(不包括底面ABCD)的面积的最大,则点C在直线OQ上,如图.
解:欲使得棱锥影子(不包括底面ABCD)的面积的最大,则点C在直线OQ上,如图.| RO |
| RQ |
| SO |
| PQ |
| x |
| x+3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
3
| ||
| 8 |
3
| ||
| 8 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com