
 ; ②{x|x∈R,x≠0};③
; ②{x|x∈R,x≠0};③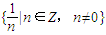 ; ④整数集Z
; ④整数集Z 中的元素是极限为1的数列,
中的元素是极限为1的数列, ,
, 的时候,不存在满足得0<|x|<a的x,
的时候,不存在满足得0<|x|<a的x,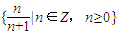 的聚点
的聚点 (实际上任意比a小得数都可以),使得0<|x|=
(实际上任意比a小得数都可以),使得0<|x|= <a
<a 中的元素是极限为0的数列,
中的元素是极限为0的数列, ,使0<|x|=
,使0<|x|= <a
<a 的聚点
的聚点

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| n |
| n+1 |
| 1 |
| n |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| n |
| n+1 |
| 1 |
| n |
| A.②③ | B.①④ | C.①③ | D.①②④ |
查看答案和解析>>
科目:高中数学 来源:2011年北京大学附中高三适应性训练数学试卷(理科)(解析版) 题型:选择题
 ; ②{x|x∈R,x≠0};③
; ②{x|x∈R,x≠0};③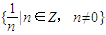 ; ④整数集Z
; ④整数集Z查看答案和解析>>
科目:高中数学 来源:2011年北京大学附中高三适应性训练数学试卷(文科)(解析版) 题型:选择题
 ; ②{x|x∈R,x≠0};③
; ②{x|x∈R,x≠0};③ ; ④整数集Z
; ④整数集Z查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com