
分析 (1)a=2时,集合A、B为两确定的集合,利用集合运算求解;
(2)a>$\frac{1}{3}$时,根据元素x∈A是x∈B的必要条件,说明B⊆A,确定端点的大小,结合数轴分析条件求解即可.
解答 解:(1)当a=2时,A=(2,7),B=(4,5),∴A∪B={a|2<a<7};
(2)当a>$\frac{1}{3}$时,3a+1>2,∴A=(2,3a+1)
∵若元素x∈A是x∈B的必要条件,∴B⊆A,
∴a=1时,B=Φ,满足B⊆A;a≠1时,$\left\{\begin{array}{l}{2a≥2}\\{{a}^{2}+1≤3a+1}\end{array}\right.$,
∴1≤a≤3.
点评 本题借助充要条件等知识点考查集合运算,含有参数的数集进行交、并、补运算,要比较端点的大小.


科目:高中数学 来源: 题型:选择题
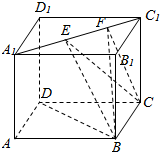 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | BD⊥CE | |
| B. | △CEF的面积为定值 | |
| C. | 四面体BCEF的体积随EF的位置的变化而变化 | |
| D. | 直线BE与CF为异面直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①与② | B. | ①与④ | C. | ②与③ | D. | ②与④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
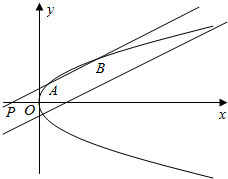 如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B
如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com