
【题目】某商场为迎接“618年中庆典,拟推出促销活动,活动规则如下:①活动期间凡在商场内购物,每满673元可参与一次现金红包抽奖,且互不影响,详细如下表:
奖项 | 一等奖 | 二等奖 |
奖金 | 200元现金红包 | 优惠餐券1张(价值50元) |
获奖率 | 30% | 70% |
②活动期间凡在商场内购物,每满2019元可参与消费返现,返现金额为实际消费金额的15%.规定每位顾客只可选择参加其中一种优惠活动.
(1)现有顾客甲在商场消费2019元,若其选择参与抽奖,求其可以获得现金红包的概率.
(2)现有100名消费金额为2019元的顾客正在等待抽奖,假如你是该商场的活动策划人,你更希望顾客参与哪项优惠活动?
【答案】(1)0.657;(2)现金抽奖活动.
【解析】
(1)记事件A为参与一次抽奖中奖,则![]() ,
,![]() ,然后消费2019元可抽奖3次,获得现金红包的概率为
,然后消费2019元可抽奖3次,获得现金红包的概率为![]()
(2)若选择返现,可算出100名顾客共需支出30285元,若选择参加抽奖,设X为其三次抽奖的获利情况,求出X的分布列,算出其期望,然后可得100名共需支出28500元,两者比较即可得出答案.
(1)记事件A为参与一次抽奖中奖,则![]() ,
,![]()
依题意,消费2019元可抽奖3次,则获得现金红包的概率为![]() ,
,
(2)由题知,若选择返现,每位顾客可获得![]() 元,
元,
所以100名顾客共需支出30285元
若选择参加抽奖,设X为其三次抽奖的获利情况,
则由题可知,X可取150,300,450,600,所以
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列如下:
P | 150 | 300 | 450 | 600 |
X | 0.343 | 0.441 | 0.189 | 0.027 |
则![]() 元,
元,
由1名顾客的平均支出为285元,则100名共需支出28500元.
因为![]() ,
,
所以作为该商场的活动策划人,更希望顾客参加现金抽奖活动.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】一个口袋中有4个白球,2个黑球,每次从袋中取出一个球.
(1)若有放回的取2次球,求第二次取出的是黑球的概率;
(2)若不放回的取2次球,求在第一次取出白球的条件下,第二次取出的是黑球的概率;
(3)若有放回的取3次球,求取出黑球次数![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,棱长为2,
中,棱长为2,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 为底面正方形
为底面正方形![]() 内一点(含边界)且
内一点(含边界)且![]() 与面
与面![]() 所成角的正切值为
所成角的正切值为![]() ,直线
,直线![]() 与面
与面![]() 的交点为
的交点为![]() ,当
,当![]() 到
到![]() 的距离最小时,则四面体
的距离最小时,则四面体![]() 外接球的表面积为___________.
外接球的表面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
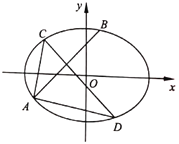
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点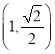 ,且椭圆的离心率为
,且椭圆的离心率为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中垂线交椭圆
的中垂线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 长的最大值;
长的最大值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,上顶点坐标为
,上顶点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)问是否存在斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 的重心分别为
的重心分别为![]() ,且以线段
,且以线段![]() 直径的圆过原点,若存在,求出直线
直径的圆过原点,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆
,圆![]() (
(![]() 为坐标原点).过点
为坐标原点).过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 交于点
交于点![]() ,与椭圆
,与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]() .
.
(1)求椭圆![]() 的方程和圆
的方程和圆![]() 的方程;
的方程;
(2)过圆![]() 上的动点
上的动点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,若直线
,若直线![]() 的斜率为
的斜率为![]() 且
且![]() 与椭圆
与椭圆![]() 相切,试判断直线
相切,试判断直线![]() 与椭圆
与椭圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com