解:(1)∵a
2,a
7是关于x的方程:
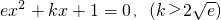
两个实根,
∴a
2a
7=

∴a
12q
7=

①
∵a
4=e,②

得a
1q
4=

=a
5∴q=e
-3∴数列的通项是a
n=e×(e
-3)
n-4=e
-3n+13(2)∵b
n=lna
n=-3n+13,
∴数列{b
n}是一个等差数列
∴数列{b
n}的前n项的和S
n是
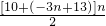
=-
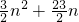
,
∴S
n=n时,有
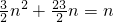
,
∴n=7,n=0(舍去)
∴n=7即n的值为7.
(3)∵b
1=10,b
2=7,b
3=4,b
4=1,b
5=-2,b
6=-5
∴c
1=280,c
2=28,c
3=-8,c
4=10,从第五项开始,这个数列的项就是负数,
∵T
1=280,
T
2=308
T
3=300
T
4=310
T
5一定小于T
4,
T
6一定小于T
5,依此类推
∴T
n的最大值310,相应的n的值是2.
分析:(1)根据数列的两项是一元二次方程根,根据根与系数的关系,表示出两个项的积,用首项和公比表示出来,同第四项作比,得到第五项,得到公比,写出数列的通项.
(2)构造出新数列,表示出新数列的通项,得到一个等差数列,根据等差数列的前n项和公式,表示出前n项和,使它等于n,解关于n的方程,得到结果.
(3)列举出数列{b
n}的前六项,进而列举出数列{c
n}的前四项,求出数列的前几项的和,观察出后面的项都是负数,只有前几项的和可能取得最大值,比较得到结果.
点评:本题考查数列的求和,考查等比数列的通项公式及等差数列的前n项和,本题解题的关键是采用列举的方法对数列的前几项的和表示出来,进行分析,注意数字的运算不要出错,本题是一个中档题目.

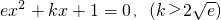 两个实根,(e是自然对数的底数)
两个实根,(e是自然对数的底数)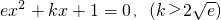 两个实根,
两个实根,
 ①
① 得a1q4=
得a1q4= =a5
=a5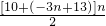 =-
=-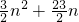 ,
,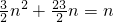 ,
,
