练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设整数是区间中的不同整数.证明：集合有这样的子集存在，它的所有元素之和能被整除.

    【答案】见解析

    【解析】

    1.若，则个整数都属于.于是，其中至少有二数相等，令.

    因，必有.

    于是能被整除.

    2.若.不妨设，考虑个整数，在其中任取三个数.若均能被整除，则

    ，

    从而，，与矛盾.

    故中至少有两个数之差不能被整除.

    不妨设与的差不能被整除，考虑个整数：

    .

    i. 若这个数关于模的余数都不同，则其中必有一个数能被整除，令此数为.若为偶数，结论成立；若为奇数，加上即构成所需要的子集.

    ii. 若这些数关于模有两个以上的数同余，则任取其中二数之差必被整除，对照这些数的表达式知，因为和不同余，故二同余的数之差必为原集合中若干数之和.不妨仍记此和为，以下讨论同i.

    注：是必要的，例如时，结论对（0，6）的子集{1，3，4}不成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称函数的一个上界.已知函数， .

    （1）若函数为奇函数，求实数的值；

    （2）在第（1）的条件下，求函数在区间上的所有上界构成的集合；

    （3）若函数在上是以3为上界的有界函数，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据气象中心观察和预测:发生于甲地的沙尘暴一直向正南方向移动，其移动速度与时间的函数图象图所示，过线段上一点作横轴的垂线，梯形在直线左侧部分的面积即为内沙尘暴所经过的路程.

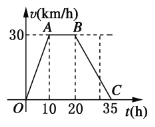
    （1） 当时，求的值；

    （2）将随变化的规律用数学关系式表示出来；

    （3）若乙城位于甲地正南方向，且距甲地，试判断这场沙尘暴是否会侵袭到乙城，如果会，在沙尘暴发生后多长时间它将侵袭到乙城?如果不会，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，解不等式；

    （2）若关于的方程在区间上有两个不等的实根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题:

    ①非零向量满足，则和的夹角为30°；

    ②将函数 的图像按向量 平移，得到函数的图像；

    ③在三角形ABC中，若 ，则三角形ABC为等腰三角形；其中正确命题的个数是（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

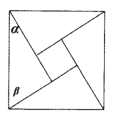
    【题目】《周髀算经》中给出了弦图，所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为，，且小正方形与大正方形面积之比为，则的值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，过点的直线的参数方程为（为参数），直线与曲线相交于，两点.

    （1）写出曲线的直角坐标方程和直线的普通方程；

    （2）若，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形为矩形， 平面， .

    （1）求证： ；

    （2）若直线平面，试判断直线与平面的位置关系，并说明理由；

    （3）若， ，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知倾斜角为的直线过点和点，点在第一象限，.

    （1）求的坐标；

    （2）若直线与两平行直线，相交于、两点，且，求实数的值；

    （3）记集合直线经过点且与坐标轴围成的面积为，，针对的不同取值，讨论集合中的元素个数.

    查看答案和解析>>

    同步练习册答案