
分析 (1)先求出b的范围,再用分析法证明即可.
(2)欲对一切x∈R,有|x+$\frac{1}{x}$|≥2,可转化成对一切满足|x|≥2的实数x,有f(x)≥0,求出$\frac{2{x}^{2}+3}{{x}^{2}+1}$的值域,再研究函数f(x)在其值域范围内的单调性,求出最大值,建立等量关系,求出b,c满足的条件.
解答 解:(1)∵b=c>0,所以f(x)=x2+bx+b,
因为函数f(x)的图象于x轴有两个不同的交点,
∴b2-4b>0,解得b>4,
∴x1=$\frac{-b-\sqrt{{b}^{2}-4b}}{2}$,x2=$\frac{-b+\sqrt{{b}^{2}-4b}}{2}$,
要证,x1<-1且x2<-1,
只要证:$\frac{-b-\sqrt{{b}^{2}-4b}}{2}$<-1且$\frac{-b+\sqrt{{b}^{2}-4b}}{2}$<-1,
只要证:-b-$\sqrt{{b}^{2}-4b}$<-2,且-b+$\sqrt{{b}^{2}-4b}$<-2,
只要证:2-b<$\sqrt{{b}^{2}-4b}$,且$\sqrt{{b}^{2}-4b}$<b-2=$\sqrt{{b}^{2}-4b+4}$
∵b>4,
∴2-b<0,
∴2-b<$\sqrt{{b}^{2}-4b}$,且$\sqrt{{b}^{2}-4b}$<b-2,
∴x1<-1且x2<-1;
(2)因为|x+$\frac{1}{x}$|≥2,依题意,对一切满足|x|≥2的实数x,有f(x)≥0.
①当f(x)=0有实根时,f(x)=0的实根在区间[-2,2]内,设f(x)=x2+bx+c,所以$\left\{\begin{array}{l}{f(-2)≥0}\\{f(2)≥0}\\{-2≤-\frac{b}{2}≤2}\end{array}\right.$,
即$\left\{\begin{array}{l}{4-2b+c≥0}\\{4+2b+c≥0}\\{-4≤b≤4}\end{array}\right.$,又$\frac{2{x}^{2}+3}{{x}^{2}+1}$=2+$\frac{1}{{x}^{2}+1}$∈(2,3],
于是,f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)的最大值为f(3)=1,即9+3b+c=1,从而c=-3b-8.
故$\left\{\begin{array}{l}{4-2b-3b-8≥0}\\{4+2b-3b-8≥0}\\{-4≤b≤4}\end{array}\right.$,解得b=-4,c=4.
②当f(x)=0无实根时,△=b2-4c<0,由二次函数性质知,
f(x)=x2+bx+c在(2,3]上的最大值只能在区间的端点处取得,
所以,当f(2)>f(3)时,f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)无最大值.
于是,f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)存在最大值的充要条件是f(2)≤f(3),
即4+2b+c≤9+3b+c,所以,b≥-5.又f($\frac{2{x}^{2}+3}{{x}^{2}+1}$)的最大值为f(3)=1,
即9+3b+c=1,从而c=-3b-8.由△=b2-4c<0,得b2+12b+32<0,即-8<b<-4.
所以b、c满足的条件为3b+c+8=0且-5≤b<-4.
综上:3b+c+8=0且-5≤b≤-4.
点评 本题主要考查了函数的单调性,以及函数恒成立问题和函数最值与几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
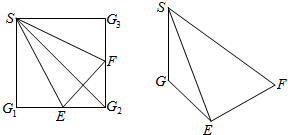 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
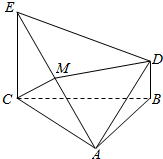 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com