Question

1．如图，三棱柱ABC-A₁B₁C₁中，侧面BB₁C₁C为菱形，B₁C的中点为O，AC=AB₁．

（1）文字叙述平面与平面垂直判定定理；
（2）求证：平面ABO⊥平面ACB₁．

Answer 1

分析 （1）通过作辅助线，作出二面角，利用定义法证明二面角的平面角的大小为90度即可得到证明；
（2）证明B₁C⊥平面ABO，即可证明平面ABO⊥平面ACB₁．

解答 （1）解：两个平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．
证明：设AB?α，AB⊥β，α∩β=CD，
则由AB?α，知AB、CD共面，
AB⊥β，CD?β，∴AB⊥CD，垂足为点B，
在平面β内过点B作直线BE⊥CD，
则∠ABE是二面角α-CD-β的平面角，
又AB⊥BE，即二面角α-CD-β是直二面角，
∴α⊥β；
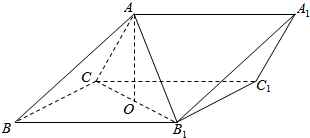
（2）证明：∵AC=AB₁，∴三角形ACB₁为等腰三角形，
∵O为B₁C的中点，
则AO⊥B₁C，
菱形BB₁C₁C，则B₁C⊥BC₁，
AO∩BC₁=O，AO，BC₁⊆平面ABO，AO⊆平面ABO
则有B₁C⊥平面ABO
又因为B₁C⊆平面ACB₁
所以平面ABO⊥平面ACB₁．

点评 本题考查平面与平面垂直判定的证明与运用，考查学生分析解决问题的能力，属于中档题．