
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
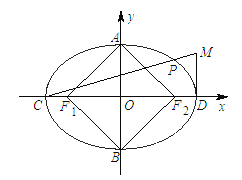
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)见解析;(Ⅲ) 存在
;(Ⅱ)见解析;(Ⅲ) 存在![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点.
的交点.
【解析】
试题(I)由于四边形为正方形,所以![]() ,由此求得椭圆方程为
,由此求得椭圆方程为![]() .(II)设出直线
.(II)设出直线![]() 的方程,联立直线方程和椭圆方程,求出
的方程,联立直线方程和椭圆方程,求出![]() 点坐标,代入
点坐标,代入![]() 可求得值为
可求得值为![]() .(III)设出
.(III)设出![]() 点的坐标,利用圆的直径所对圆周角为直角的几何性质得到
点的坐标,利用圆的直径所对圆周角为直角的几何性质得到![]() ,结合(II)将
,结合(II)将![]() 的坐标代入上式,可求得
的坐标代入上式,可求得![]() .
.
试题解析:(Ⅰ)由题意得, ![]()
![]() ,
,![]()
所以所求的椭圆方程为![]()
(Ⅱ)由(Ⅰ)知, ![]() ,
,![]()
由题意可设![]() ,
,![]() .
.
因为![]()
所以![]()
由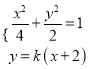 整理得:
整理得:![]()
因为![]()
所以![]() ,
,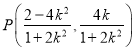
所以![]()
(Ⅲ)设![]() ,则
,则![]() .
.
若以![]() 为直径的圆恒过
为直径的圆恒过![]() ,
,![]() 的交点,则
的交点,则![]() ,
,
所以![]() 恒成立
恒成立
由(Ⅱ)可知![]() ,
,
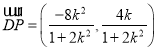 .
.
所以![]() .
.
即![]() 恒成立.
恒成立.
所以![]() .
.
所以存在![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点.
的交点.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为![]() 公里,远月点与月球表面距离为
公里,远月点与月球表面距离为![]() 公里.已知月球的直径为
公里.已知月球的直径为![]() 公里,则该椭圆形轨道的离心率约为
公里,则该椭圆形轨道的离心率约为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来大气污染防治工作得到各级部门的重视,某企业现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() ,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为
,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后当日产量
万元,除尘后当日产量![]() 时,总成本
时,总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为59万元,试求除尘后日产量为多少时,每吨产品的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 与点
与点![]() 的距离和它到直线
的距离和它到直线![]() 的距离相等,记点
的距离相等,记点![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程
的方程
(2)设点![]() ,动点
,动点![]() 在曲线
在曲线![]() 上运动时,
上运动时,![]() 的最短距离为
的最短距离为![]() ,求
,求![]() 的值以及取到最小值时点
的值以及取到最小值时点![]() 的坐标
的坐标
(3)设![]() 为曲线
为曲线![]() 的任意两点,满足
的任意两点,满足![]() (
(![]() 为原点),试问直线
为原点),试问直线![]() 是否恒过一个定点?如果是,求出定点坐标;如果不是,说明理由
是否恒过一个定点?如果是,求出定点坐标;如果不是,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业用180万元购买一套新设备,该套设备预计平均每年能给企业带来100万元的收入,为了维护设备的正常运行,第一年需要各种维护费用10万元,且从第二年开始,每年比上一年所需的维护费用要增加10万元
(1)求该设备给企业带来的总利润![]() (万元)与使用年数
(万元)与使用年数![]() 的函数关系;
的函数关系;
(2)试计算这套设备使用多少年,可使年平均利润最大?年平均利润最大为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+2|x+1|.
(1)当a=2时,解不等式f(x)>4.
(2)若不等式f(x)<3x+4的解集是{x|x>2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
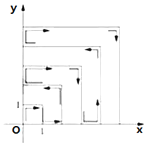
【题目】如图,一个粒子的起始位置为原点,在第一象限内于两正半轴上运动,第一秒运动到(0,1),而后它接着按图示在![]() 轴、
轴、![]() 轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过
轴的垂直方向来回运动,且每秒移动一个单位长度,如图所示,经过![]() 秒时移动的位置设为
秒时移动的位置设为![]() ,那么经过2019秒时,这个粒子所处的位置的坐标是______.
,那么经过2019秒时,这个粒子所处的位置的坐标是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业研制出一种型号为A的精密数控车床,A型车床为企业创造的价值逐年减少(以投产一年的年初到下一年的年初为A型车床所创造价值的第一年).若第 1 年A型车床创造的价值是250万元,且第1年至第6年,每年A型车床创造的价值减少30万元;从第7年开始,每年A型车床创造的价值是上一年价值的 50%.现用![]() (
(![]() )表示A型车床在第n年创造的价值.
)表示A型车床在第n年创造的价值.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)记![]() 为数列
为数列![]() 的前n项的和
的前n项的和![]()
![]() ,企业经过成本核算,若
,企业经过成本核算,若![]() 万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列
万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列![]() 是单调递减数列,则数列
是单调递减数列,则数列![]() 也是单调递减数列).
也是单调递减数列).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com