
【题目】已知函数f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)对任意![]() ,
,![]() 都有恒成立,求实数a的取值范围;
都有恒成立,求实数a的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)![]() (2)(
(2)(![]() (3)见证明
(3)见证明
【解析】
(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律确定函数单调性,最后根据函数单调性确定最小值取法;(2)先分离不等式,转化为对应函数最值问题,利用导数求对应函数最值即得结果;(3)构造两个函数,再利用两函数最值关系进行证明.
(1)![]()
当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增,所以函数f(x)的最小值为f(
单调递增,所以函数f(x)的最小值为f(![]() )=
)=![]() ;
;
(2)因为![]() 所以问题等价于
所以问题等价于![]() 在
在![]() 上恒成立,
上恒成立,
记![]() 则
则![]() ,
,
因为![]() ,
,
令![]()
![]() 函数f(x)在(0,1)上单调递减;
函数f(x)在(0,1)上单调递减;
![]() 函数f(x)在(1,+
函数f(x)在(1,+![]() )上单调递增;
)上单调递增;
![]() 即
即![]() ,
,
即实数a的取值范围为(![]() .
.
(3)问题等价于证明![]()
由(1)知道![]()
![]() ,令
,令![]()
![]() 函数
函数![]() 在(0,1)上单调递增;
在(0,1)上单调递增;
![]() 函数
函数![]() 在(1,+
在(1,+![]() )上单调递减;
)上单调递减;
所以{![]() ,
,
因此![]() ,因为两个等号不能同时取得,所以
,因为两个等号不能同时取得,所以![]()
即对一切![]() ,都有
,都有![]() 成立.
成立.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量![]() 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着现代社会的发展,我国对于环境保护越来越重视,企业的环保意识也越来越强.现某大型企业为此建立了5套环境监测系统,并制定如下方案:每年企业的环境监测费用预算定为1200万元,日常全天候开启3套环境监测系统,若至少有2套系统监测出排放超标,则立即检查污染源处理系统;若有且只有1套系统监测出排放超标,则立即同时启动另外2套系统进行1小时的监测,且后启动的这2套监测系统中只要有1套系统监测出排放超标,也立即检查污染源处理系统.设每个时间段(以1小时为计量单位)被每套系统监测出排放超标的概率均为![]() ,且各个时间段每套系统监测出排放超标情况相互独立.
,且各个时间段每套系统监测出排放超标情况相互独立.
(1)当![]() 时,求某个时间段需要检查污染源处理系统的概率;
时,求某个时间段需要检查污染源处理系统的概率;
(2)若每套环境监测系统运行成本为300元/小时(不启动则不产生运行费用),除运行费用外,所有的环境监测系统每年的维修和保养费用需要100万元.现以此方案实施,问该企业的环境监测费用是否会超过预算(全年按9000小时计算)?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王想在某市一住宅小区买套新房,据了解,该小区有若干栋互相平行的平顶楼房,每栋楼房有15层,每层楼高为3米,顶楼有1米高的隔热层,两楼之间相距60米.小王不想买最前面和最后面的楼房,但希望所买楼层全年每天正午都能晒到太阳.为此,小王查找了有关地理资料,获得如下一些信息:①该市的纬度(地面一点所在球半径与赤道平面所成的角)为北纬![]() ;②正午的太阳直射北回归线(太阳光线与赤道平面所成的角为
;②正午的太阳直射北回归线(太阳光线与赤道平面所成的角为![]() )时,物体的影子最短,直射南回归线(太阳光线与赤道平面所成的角为
)时,物体的影子最短,直射南回归线(太阳光线与赤道平面所成的角为![]() )时,物体的影子最长,那么小王买房的最低楼层应为( )
)时,物体的影子最长,那么小王买房的最低楼层应为( )
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).设
).设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
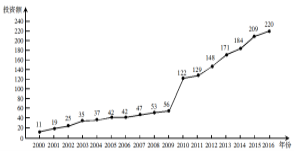
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com