
【题目】已知函数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ;
;
(2)令![]()
![]() 是函数
是函数![]() 图象上任意两点,且满足
图象上任意两点,且满足![]() 求实数
求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .(2)
.(2)![]() (3)
(3)![]() .
.
【解析】
试题分析:(1)先求导数![]() ,再求导函数零点
,再求导函数零点![]() ,根据零点与定义区间位置关系分类讨论函数单调性:当
,根据零点与定义区间位置关系分类讨论函数单调性:当![]() 时,
时,![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数,最后根据单调性确定函数最小值(2)先转化不等式
上为增函数,最后根据单调性确定函数最小值(2)先转化不等式![]() 不妨取
不妨取![]() ,则
,则![]() ,即
,即![]() 恒成立,即
恒成立,即![]() 在
在![]() 上单调递增,然后利用导数研究函数单调性:
上单调递增,然后利用导数研究函数单调性:![]() 在
在![]() 恒成立.最后利用变量分离转化为对应函数最值,求参数.(3)不等式有解问题与恒成立问题一样,先利用变量分离转化为对应函数最值,
恒成立.最后利用变量分离转化为对应函数最值,求参数.(3)不等式有解问题与恒成立问题一样,先利用变量分离转化为对应函数最值,![]() 的最大值,再利用导数求函数
的最大值,再利用导数求函数![]() 的最值,这要用到二次求导,才可确定函数单调性:
的最值,这要用到二次求导,才可确定函数单调性:![]() 在
在![]() 上单调递增,进而确定函数最值
上单调递增,进而确定函数最值
试题解析:解(1)![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数,
上为增函数,
![]() 的最小值为
的最小值为![]() .
.
综上,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)![]() ,对于任意的
,对于任意的![]() ,不妨取
,不妨取![]() ,则
,则![]() ,
,
则由![]() 可得
可得![]() ,
,
变形得![]() 恒成立,
恒成立,
令![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 恒成立.
恒成立.
![]() ,当且仅当
,当且仅当![]() 时取
时取![]() ,
,
![]() .
.
(3)![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() 使得
使得![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
令![]() ,则由
,则由![]() 可得
可得![]() 或
或![]() (舍)
(舍)
当![]() 时
时![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时
时![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
![]()
![]() 在
在![]() 上恒成立.
上恒成立.
![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,即
,即![]() .
.
![]() 实数
实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查者中恰有1名对手机游戏无兴趣的概率.
附: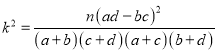
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.
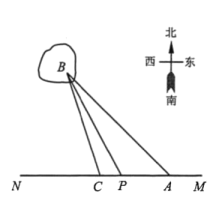
(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中无理数
,其中无理数![]() .
.
(Ⅰ)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的极值点有三个,最小的记为
的极值点有三个,最小的记为![]() ,最大的记为
,最大的记为![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是各项均为正数的等比数列,
是各项均为正数的等比数列,![]() 是等差数列,且
是等差数列,且![]() .
.
(I)求![]() 和
和![]() 的通项公式;
的通项公式;
(II)设数列![]() 满足
满足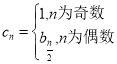 ,求
,求![]() ;
;
(III)对任意正整数![]() ,不等式
,不等式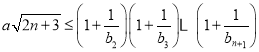 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com